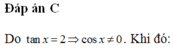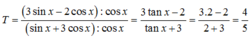Các câu hỏi tương tự
Cho cos x + sin x = 3/4. Tính giá trị biểu thức A= |sin x - cos x|
Giải các PT sau:1. dfrac{left(2cos2x-1right)left(sin x-3right)}{sin x}0 2.dfrac{3left(sin x+cos xright)}{sin x-cos x}2+2cos x3.dfrac{3left(sin x+tan xright)}{tan x-sin x}-2cos x24. 1+sin x+cos x+sin2x+cos2x05. 2sin xleft(1+cos2xright)+sin2x1+2cos x
Đọc tiếp
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)
chứng minh rằng
a) tanx(cot\(^2\)x - 1) = cotx(1 - tan\(^2\)x)
b) tan\(^2\)x - sin\(^2\)x = tan\(^2\)x.sin\(^2\)x
c) \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}\) - cos\(^2\)x = - cos\(^4\)x
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
.
cos
x
2
-
3
.
sin
x...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
giải phương trình
a) \(sin\left(x-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
b) \(cos\left(x+\dfrac{\pi}{4}\right)=cos\dfrac{3\pi}{4}\)
c) \(tan2x=tan\left(x+\dfrac{\pi}{3}\right)\)
d) \(cot2x=-\dfrac{\sqrt{3}}{3}\)
cho \(sinx\) = \(\dfrac{1}{5}\) và \(\dfrac{\pi}{2}\) < x < \(\pi\) tính
a) sin2x, cos2x, tan2x, cot2x
b) \(sin\left(x-\dfrac{\pi}{6}\right)\)
c) \(cos\left(x-\dfrac{\pi}{3}\right)\)
d) \(tan\left(x-\dfrac{\pi}{4}\right)\)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
cos
x
+
2
.
sin
x
+
3
2
.
cos
x...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11
cho cosx = \(-\dfrac{1}{4}\) và \(\dfrac{\pi}{2}\) < x < \(\pi\) tính
a) sin2x, cos2x, tan2x, cot2x
b) \(sin\left(x+\dfrac{5\pi}{6}\right)\)
c) \(cos\left(\dfrac{\pi}{6}-x\right)\)
d) \(tan\left(x+\dfrac{\pi}{3}\right)\)