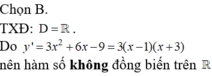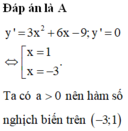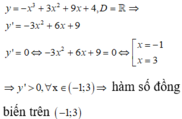3x2 + ( -9x ) + 10x = 4 + 15

Những câu hỏi liên quan
Thực hiện phép tính: a) 4n²/17n⁴ × ( - 7m² / 12n ) b) 3x - 1 / 10x² + 2x × 25x² +10x +1/ 1 - 9x² c) 27 - a³ / 5a + 10 ÷ a - 3 / 3a + 6 d) x² - 1 / x² + 2x - 15 ÷ x² +5x +4 / x² -10x +21
a) \(\dfrac{4n^2}{17n^4}\cdot\dfrac{-7n^2}{12n}\) \(\left(n\ne0\right)\)
\(=\dfrac{4n^2\cdot-7n^2}{17n^4\cdot12n}\)
\(=\dfrac{-28n^4}{204n^5}\)
\(=\dfrac{-7}{51n}\)
b) \(\dfrac{3x-1}{10x^2+2x}\cdot\dfrac{25x^2+10x+1}{1-9x^2}\) \(\left(x\ne\pm\dfrac{1}{3};x\ne0;x\ne-\dfrac{1}{5}\right)\)
\(=\dfrac{3x-1}{2x\left(5x+1\right)}\cdot\dfrac{\left(5x+1\right)^2}{\left(1-3x\right)\left(3x+1\right)}\)
\(=\dfrac{-\left(1-3x\right)\left(5x+1\right)^2}{2x\left(5x+1\right)\left(1-3x\right)\left(1+3x\right)}\)
\(=\dfrac{-\left(5x+1\right)}{2x\left(1+3x\right)}\)
\(=-\dfrac{5x+1}{6x^2+2x}\)
c) \(\dfrac{27-a^3}{5a+10}:\dfrac{a-3}{3a+6}\) \(\left(a\ne-2;a\ne3\right)\)
\(=\dfrac{\left(3-a\right)\left(9+3a+a^2\right)}{5\left(a+2\right)}\cdot\dfrac{3\left(a+2\right)}{a-3}\)
\(=\dfrac{-\left(a-3\right)\left(a^2+3a+9\right)\cdot3\left(a+2\right)}{5\left(a+2\right)\left(a-3\right)}\)
\(=\dfrac{-3\left(a^2+3x+9\right)}{5}\)
\(=-\dfrac{3x^2+9x+27}{5}\)
d) \(\dfrac{x^2-1}{x^2+2x-15}:\dfrac{x^2+5x+4}{x^2-10x+21}\) \(\left(x\ne3;x\ne-5;x\ne-1;x\ne-4\right)\)
\(=\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-3\right)\left(x+5\right)}:\dfrac{\left(x+1\right)\left(x+4\right)}{\left(x-3\right)\left(x-7\right)}\)
\(=\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-3\right)\left(x+5\right)}\cdot\dfrac{\left(x-3\right)\left(x-7\right)}{\left(x+1\right)\left(x+4\right)}\)
\(=\dfrac{\left(x+1\right)\left(x-7\right)}{\left(x+5\right)\left(x+4\right)}\)
Đúng 3
Bình luận (0)
Cho hàm số
y
x
3
+
3
x
2
-
9
x
+
15
. Khẳng định nào sau đây là sai? A. Hàm số đồng biến trên
-
9
;
-
5
B. Hàm số nghịch biến trên khoảng
-
3
;
1...
Đọc tiếp
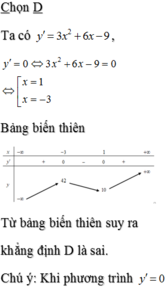
Cho hàm số y = x 3 + 3 x 2 - 9 x + 15 . Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên - 9 ; - 5
B. Hàm số nghịch biến trên khoảng - 3 ; 1
C. Hàm số đồng biến trên khoảng 5 ; + ∞
D. Hàm số đồng biến trên R
Tính giá trị của phân thức:a)
x
2
−
1
2
x
2
−
3
x
+
1
với
x
≠
1
và
x
≠
1
2
tại
2...
Đọc tiếp
Tính giá trị của phân thức:
a) x 2 − 1 2 x 2 − 3 x + 1 với x ≠ 1 và x ≠ 1 2 tại 2 x + 1 = 3 ;
b) 3 x 2 − 10 x + 3 x 2 − 4 x + 3 với x ≠ 2 ; x ≠ 3 tại x 2 − 8 x + 15 = 0 .
Cho hàm số
y
x
3
+
3
x
2
-
9
x
+
15
. Khẳng định nào sau đây là khẳng định sai? A. Hàm số nghịch biến trên khoảng (-3;1). B. Hàm số đồng biến trên
ℝ
. C. Hàm số đồng biến trên (-9;5) D. Hàm số đồng biến trên khoảng
(
5...
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 - 9 x + 15 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1).
B. Hàm số đồng biến trên ℝ .
C. Hàm số đồng biến trên (-9;5)
D. Hàm số đồng biến trên khoảng ( 5 ; + ∞ )
Bài 1 Tìm x
a ) |3x-7|+|15-3x|=8
b) |4x-98|+4|2-x|=90
Bài 2 Thu gọn
a) M= |9x-2|+4-10x
b) N= 7-|6-5x|+9x
Bài 1:
a: \(\Leftrightarrow\left|3x-7\right|+\left|3x-15\right|=8\)
TH1: x<7/3
Pt sẽ là \(7-3x+15-3x=8\)
=>22-6x=8
=>6x=14
hay x=7/3(loại)
TH2: 7/3<=x<5
Pt sẽ là \(3x-7+15-3x=8\)
=>8=8(luôn đúng)
TH3: x>=5
Pt sẽ là 3x-7+3x-15=8
=>6x-22=8
hay x=5(nhận)
b: \(\Leftrightarrow\left|4x-98\right|+\left|4x-8\right|=90\)
TH1: x<2
Pt sẽ là 8-4x+98-4x=90
=>106-8x=90
=>x=2(loại)
TH2: 2<=x<49/2
Pt sẽ là 4x-8+98-4x=90
=>90=90(luôn đúng)
TH3: x>=49/2
Pt sẽ là 4x-8+4x-98=90
=>8x-106=90
=>8x=196
hay x=24,5(nhận)
Đúng 0
Bình luận (0)
Gỉai các phương trình sau;
a, 3x2 - 8x2 - 2x + 3 = 0
b, x3 - 4x2 + 7x - 6 = 0
c, 2x3 + 7x2 + 7x + 2 = 0
d, 2x3 - 9x + 2 = 0
e, 8x3 - 4x2 + 10x - 5 = 0
a, 3x2 - 8x2 - 2x+3=0
2x(3-8) - 2x+3=0
2x5 - 2x+3=0
2x5 - 2x=0-3=
2x5 - 2x=-3
2x(5-x)=-3
5-x=-3/2
5-x=1,5
x=5-1,5
x=3,5
Đúng 0
Bình luận (0)
3,5 nha bn
chúc bn học tốt
happy new year
Đúng 0
Bình luận (0)
Hàm số
y
x
3
+
3
x
2
-
9
x
+
4
nghịch biến trên: A.
(
-
3
;
+
∞
)
B.
(
-
∞
;
1
)
C. (3;1) D.
(
-
∞
;
-
3
)
;
(
1
;
+
∞
)
Đọc tiếp
Hàm số y = x 3 + 3 x 2 - 9 x + 4 nghịch biến trên:
A. ( - 3 ; + ∞ )
B. ( - ∞ ; 1 )
C. (3;1)
D. ( - ∞ ; - 3 ) ; ( 1 ; + ∞ )
Hàm số
y
-
x
3
+
3
x
2
+
9
x
+
4
đồng biến trên khoảng: A.
-
1
;
3
B.
-
3
;
1
C.
-
∞
;
-...
Đọc tiếp
Hàm số y = - x 3 + 3 x 2 + 9 x + 4 đồng biến trên khoảng:
A. - 1 ; 3
B. - 3 ; 1
C. - ∞ ; - 3
D. 3 ; + ∞
Hàm số y = - x 3 + 3 x 2 + 9 x + 4 đồng biến trên khoảng
A. ( - ∞ ; - 3 )
B. ( - 1 ; 3 )
C. (3;+ ∞ )
D.(-3;1)
Đáp án là B.
• Tập xác định: D = ℝ ; y , = - 3 x 2 + 6 x + 9 ; cho y , = 0 ⇔ x = - 1 x = 3
• Xét dấu đạo hàm:
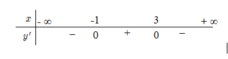
Đúng 0
Bình luận (0)