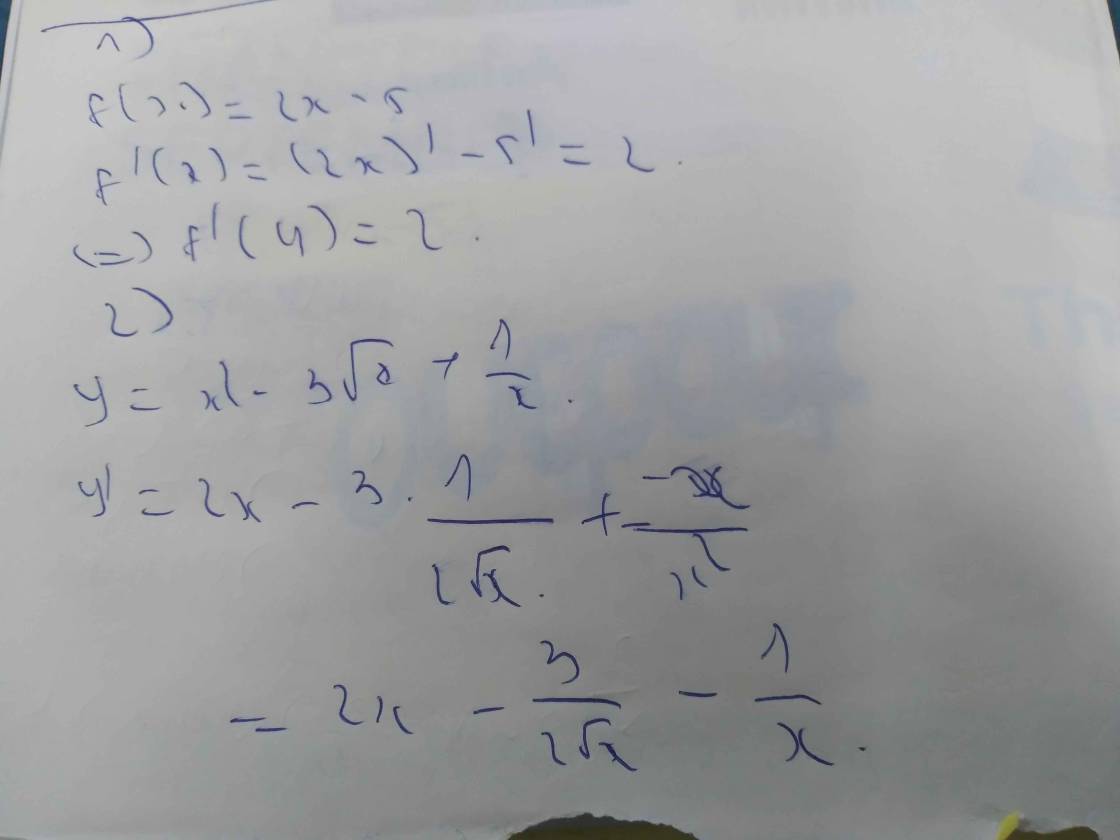\(\Rightarrow f\left(x\right)=\dfrac{7}{4}x+\dfrac{1}{8}x+\dfrac{1}{8}x+\dfrac{8}{x^2}\)

Áp dụng bđt Cô-si :

\(\dfrac{1}{8}x+\dfrac{1}{8}x+\dfrac{8}{x^2}\ge3\sqrt[3]{\dfrac{1}{8}x\cdot\dfrac{1}{8}x\cdot\dfrac{8}{x^2}}=\dfrac{3}{2}\)

\(\Rightarrow f\left(x\right)=\dfrac{7}{4}x+\dfrac{1}{8}x+\dfrac{1}{8}x+\dfrac{8}{x^2}\ge7+\dfrac{3}{2}=\dfrac{17}{2}\)

Dấu bằng xảy ra \(\Leftrightarrow x=4\)

\(f\left(x\right)=\dfrac{x}{8}+\dfrac{x}{8}+\dfrac{8}{x^2}+\dfrac{7}{4}x\ge3\sqrt[3]{\dfrac{8x^2}{64x^2}}+\dfrac{7}{4}.4=\dfrac{17}{2}\)

Dấu "=" xảy ra khi \(x=4\)

\(y=\dfrac{x+3}{4}+\dfrac{9}{x-1}=\dfrac{x-1}{4}+\dfrac{9}{x-1}+1\)

\(y\ge2\sqrt{\dfrac{9\left(x-1\right)}{4\left(x-1\right)}}+1=4\)

\(y_{min}=4\) khi \(x=7\)

1.

\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{2^2}{x}+\dfrac{1}{1-x}-1\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)

\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)

2.

\(f\left(x\right)=\dfrac{1}{x}+\dfrac{1}{1-x}\ge\dfrac{4}{x+1-x}=4\)

\(f\left(x\right)_{min}=4\) khi \(x=\dfrac{1}{2}\)

x=23x=23

2.

x=12

a:Đặt (d1): y=2x-3

Tọa độ giao điểm của (d1) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=0\end{matrix}\right.\)

Tọa độ giao điểm của (d1) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-3=0-3=-3\end{matrix}\right.\)

b: Đặt (d2): \(y=-\dfrac{3}{4}x\)

Tọa độ giao điểm của (d2) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{3}{4}x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)

Tọa độ giao điểm của (d2) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{3}{4}x=-\dfrac{3}{4}\cdot0=0\end{matrix}\right.\)

c: Đặt \(\left(d3\right):y=2x^2\)

Tọa độ giao điểm của (d3) với trục Ox là:

\(\left\{{}\begin{matrix}2x^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=0\\y=2x^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)

Tọa độ giao điểm của (d3) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)

d: Đặt (d4): \(y=\dfrac{x+1}{x-2}\)

ĐKXĐ: x<>2

Tọa độ giao điểm của (d4) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\y=\dfrac{x+1}{x-2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)

Tọa độ giao điểm của (d4) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{x+1}{x-2}=\dfrac{0+1}{0-2}=\dfrac{1}{-2}=-\dfrac{1}{2}\end{matrix}\right.\)

e: Đặt (d5): \(y=x-2+\dfrac{1}{x}\)

ĐKXĐ: x<>0

Vì hàm số không đi qua điểm có hoành độ là x=0 nên (d5) sẽ không cắt trục Oy

Tọa độ giao điểm của (d5) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\x-2+\dfrac{1}{x}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x+1=0\\y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)

f: Đặt (d6): \(y=x^2+2x-5\)

Tọa độ giao điểm của (d6) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=x^2+2x-5=0^2+2\cdot0-5=-5\end{matrix}\right.\)

Tọa độ giao điểm của (d6) với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\x^2+2x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x^2+2x+1-6=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\\left(x+1\right)^2=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x+1=\sqrt{6}\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x+1=-\sqrt{6}\end{matrix}\right.\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=\sqrt{6}-1\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x=-\sqrt{6}-1\end{matrix}\right.\end{matrix}\right.\)

1) \(f\left(x\right)=2x-5\)

\(f'\left(x\right)=2\)

\(\Rightarrow f'\left(4\right)=2\)

2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)

\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)

3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)

\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)

\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

h: ĐKXĐ: |x+1|-|x-2|<>0

=>|x+1|<>|x-2|

=>x-2<>x+1 và x+1<>-x+2

=>2x<>1

=>x<>1/2

g: ĐKXĐ: x+1>0 và x+2>=0 và x^2-4<>0

=>x>-2 và x>-1 và x<>2; x<>-2

=>x>-1; x<>2

f: ĐKXĐ: x+1>=0 và 7-2x>=0 và x+1<>7-2x

=>3x<>6 và -1<=x<=7/2

=>x<>2 và -1<=x<=7/2

f. 

\(x+1>0\) và \(7-2x>0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x>-1\\x< \dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow\) TXĐ: \(D=(-1;\dfrac{7}{2})\)

g.

\(x+1>0\) và \(x^2-4\ne0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x>-1\\x\ne2\\x\ne-2\end{matrix}\right.\)

\(\Rightarrow\) TXĐ: \(D=\left(-1;+\infty\right)\backslash2\)

Lời giải:

\(\int f(x)dx=\int \frac{x^2+2x}{x+1}dx=\int \frac{(x+1)^2-1}{x+1}dx=\int (x+1-\frac{1}{x+1})dx\)

\(=\int (x+1)dx-\int \frac{1}{x+1}dx=\frac{x^2}{2}+x-\ln |x+1|+c\)

(1)

a) x=\(\dfrac{-1}{12}-\dfrac{2}{3}\)=\(\dfrac{-3}{4}\)

b) 2x+1=3 => 2x=3-1=2 => x=1

(2)

f(2)=2.2²+4=12

f(-1)=2.(-1)²+4=6

(1)

a) \(x+\dfrac{2}{3}=-\dfrac{1}{12}\\ \Rightarrow x=-\dfrac{1}{12}-\dfrac{2}{3}\\ \Rightarrow x=\dfrac{-1}{12}-\dfrac{8}{12}\\ \Rightarrow x=-\dfrac{9}{12}=-\dfrac{3}{4}\)

Vậy \(x=-\dfrac{3}{4}\)

b) \(\left(2x+1\right)^2=9\\ \Rightarrow\left(2x+1\right)^2=3^2=\left(-3\right)^2\\ \Rightarrow\left[{}\begin{matrix}2x+1=3\\2x+1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=2\\2x=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Vậy \(x\in\left\{-2;1\right\}\)

(2)

\(y=f\left(x\right)=2x^2+4\\ f\left(2\right)=2\cdot2^2+4=8+4=12\\ f\left(-1\right)=2\cdot\left(-1\right)^2+4=2+4=6\)

Vậy \(f\left(2\right)=12\\ f\left(-1\right)=6\)