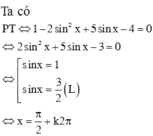a/

\(\Leftrightarrow cos2x=sin3x\)

\(\Leftrightarrow cos2x=cos\left(\frac{\pi}{2}-3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-3x+k2\pi\\2x=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k2\pi}{5}\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

b/

\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+1\right)\left(sin^2x-2sinx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\frac{1}{2}\\sinx=1-\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow x=...\)

c/

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1+cos\left(\frac{\pi}{2}-2x\right)\)

\(\Leftrightarrow1-3sin^2x.cos^2x=1+sin2x\)

\(\Leftrightarrow-\frac{3}{4}sin^22x=sin2x\)

\(\Leftrightarrow3sin^22x+4sin2x=0\)

\(\Leftrightarrow sin2x\left(3sin2x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sin2x=-\frac{4}{3}\left(l\right)\end{matrix}\right.\)

\(\Rightarrow x=\frac{k\pi}{2}\)

\(\Leftrightarrow1-5sin\left(\frac{x}{2}\right)+2-2sin^2\left(\frac{x}{2}\right)=0\)

Đặt \(sin\left(\frac{x}{2}\right)=t\Rightarrow\left|t\right|\le1\)

Pt trở thành:

\(-2t^2-5t+3=0\Rightarrow\left[{}\begin{matrix}t=-3\left(l\right)\\t=\frac{1}{2}\end{matrix}\right.\)

\(\Rightarrow sin\left(\frac{x}{2}\right)=\frac{1}{2}=sin\left(\frac{\pi}{6}\right)\)

\(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}=\frac{\pi}{6}+k2\pi\\\frac{x}{2}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k4\pi\\x=\frac{5\pi}{3}+k4\pi\end{matrix}\right.\)

Ta có: \(tan\alpha=2\Leftrightarrow\dfrac{sin\alpha}{cos\alpha}=2\Leftrightarrow sin\alpha=2cos\alpha\)

A = \(\dfrac{16cos^2\alpha+6cos^2\alpha}{20cos^2\alpha-2cos^2\alpha}=\dfrac{22cos^2\alpha}{18cos^2\alpha}=\dfrac{11}{9}\)

a/

\(\Leftrightarrow3\left(1-sin^22x\right)+4sin2x-4=0\)

\(\Leftrightarrow-3sin^22x+4sin2x-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=\frac{1}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\end{matrix}\right.\)

b/

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=\frac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow2\left(1-cos^2x\right)-\left(2+\sqrt{3}\right)cosx-2-\sqrt{3}=0\)

\(\Leftrightarrow2cos^2x+\left(2+\sqrt{3}\right)cosx+\sqrt{3}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\cosx=-\frac{\sqrt{3}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\pm\frac{\pi}{6}+k2\pi\\\end{matrix}\right.\)

d/

\(-2\left(1-2sin^22x\right)-2\left(1-\sqrt{3}\right)sin2x-\sqrt{3}+2=0\)

\(\Leftrightarrow4sin^22x-2\left(1-\sqrt{3}\right)sin2x-\sqrt{3}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sinx=-\frac{\sqrt{3}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=-\frac{\pi}{3}+k2\pi\\x=\frac{4\pi}{3}+k2\pi\end{matrix}\right.\)

f/

\(\Leftrightarrow4\left(1-2sin^2\frac{x}{2}\right)-5sin\frac{x}{2}=1\)

\(\Leftrightarrow8sin^2\frac{x}{2}+5sin\frac{x}{2}-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\frac{x}{2}=-1\\sin\frac{x}{2}=\frac{3}{8}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\pi+k4\pi\\x=2arcsin\left(\frac{3}{8}\right)+k4\pi\\x=2\pi-2arcsin\left(\frac{3}{8}\right)+k4\pi\end{matrix}\right.\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=\frac{2}{5}\)

\(\Rightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=arcsin\left(\frac{2}{5}\right)+k2\pi\\2x-\frac{\pi}{4}=\pi-arcsin\left(\frac{2}{5}\right)+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+\frac{1}{2}arcsin\left(\frac{2}{5}\right)+k\pi\\x=\frac{5\pi}{8}-\frac{1}{2}arcsin\left(\frac{2}{5}\right)+k\pi\end{matrix}\right.\)

Với \(cosx=0\) không phải nghiệm

Với \(cosx\ne0\) , chia 2 vế cho \(cos^3x\) ta được:

\(tan^3x-5tan^2x-3tanx+3=0\)

\(\Leftrightarrow\left(tanx+1\right)\left(tan^2x-6tanx+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3-\sqrt{6}\\tanx=3+\sqrt{6}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3-\sqrt{6}\right)+k\pi\\x=arctan\left(3+\sqrt{6}\right)+k\pi\end{matrix}\right.\)

Đáp án D

\(\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)=sin4x\)

\(\Leftrightarrow cos^2x-sin^2x=sin4x\)

\(\Leftrightarrow cos2x=sin4x=cos\left(\frac{\pi}{2}-4x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-4x+k2\pi\\2x=4x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k\pi}{3}\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\)

\(2cos^2x-1=sin6x\)

\(\Leftrightarrow cos2x=sin6x=cos\left(\frac{\pi}{2}-6x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-6x+k2\pi\\2x=6x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{16}+\frac{k\pi}{4}\\x=\frac{\pi}{8}+\frac{k\pi}{2}\end{matrix}\right.\)

\(2\left(cos^2x-1\right)=sinx.cos3x\)

\(\Leftrightarrow-2sin^2x=sinx.cos3x\)

\(\Leftrightarrow sinx.cos3x+2sin^2x=0\)

\(\Leftrightarrow sinx\left(cos3x+2sinx\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos3x+2sinx=0\left(1\right)\end{matrix}\right.\)

Bạn có ghi nhầm đề ko nhỉ, pt (1) dù giải được nhưng khá khó đấy, phải vận dụng công thức nhân 3 và nghiệm ko hề đẹp

\(cos^4x+sin^4x=1+\frac{1}{2}sin4x\)

\(\Leftrightarrow\left(cos^2x+sin^2x\right)^2-2\left(sinx.cosx\right)^2=1+\frac{1}{2}sin4x\)

\(\Leftrightarrow1-\frac{1}{2}sin^22x=1+\frac{1}{2}sin4x\)

\(\Leftrightarrow sin4x+sin^22x=0\)

\(\Leftrightarrow2sin2x.cos2x+sin^22x=0\)

\(\Leftrightarrow sin2x\left(2cos2x+sin2x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}sin2x=0\Rightarrow x=\frac{k\pi}{2}\\2cos2x+sin2x=0\left(1\right)\end{matrix}\right.\)

Xét (1)

\(\Leftrightarrow\frac{1}{\sqrt{5}}sin2x+\frac{2}{\sqrt{5}}cos2x=0\)

Đặt \(cosa=\frac{1}{\sqrt{5}}\) với \(a\in\left[0;\pi\right]\)

\(\Rightarrow sin2x.cosa+cos2x.sina=0\)

\(\Leftrightarrow sin\left(2x+a\right)=0\)

\(\Rightarrow2x+a=k\pi\Rightarrow x=-\frac{a}{2}+\frac{k\pi}{2}\)