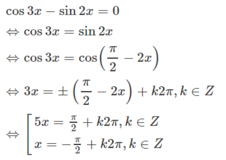1.

\(\Leftrightarrow cos3x+sin3x-2sin3x.cos3x=0\)

\(\Leftrightarrow cos3x+sin3x-\left(2sin3x.cos3x+1\right)+1=0\)

\(\Leftrightarrow cos3x+sin3x-\left(sin3x+cos3x\right)^2+1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin3x+cos3x=\frac{\sqrt{5}+1}{2}\\sin3x+cos3x=\frac{1-\sqrt{5}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(3x+\frac{\pi}{4}\right)=\frac{\sqrt{10}+\sqrt{2}}{4}>1\left(l\right)\\sin\left(3x+\frac{\pi}{4}\right)=\frac{\sqrt{2}-\sqrt{10}}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{4}=arcsin\left(\frac{\sqrt{2}-\sqrt{10}}{4}\right)+k2\pi\\3x+\frac{\pi}{4}=\pi-arcsin\left(\frac{\sqrt{2}-\sqrt{10}}{4}\right)+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow x=...\)

2.

\(\Leftrightarrow sinx-\left(1+cosx\right)+sin2x=-2\)

\(\Leftrightarrow sinx-cosx+1+sin2x=0\)

\(\Leftrightarrow sinx-cosx-\left(1-2sinx.cosx\right)+2=0\)

\(\Leftrightarrow sinx-cosx-\left(sinx-cosx\right)^2+2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=-1\\sinx-cosx=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\\sin\left(x-\frac{\pi}{4}\right)=\sqrt{2}>1\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x-\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow x=...\)

\(\Leftrightarrow2sinx+cos3x+sin2x-sin4x-1=0\)

\(\Leftrightarrow2sinx-1+cos3x-2cos3x.sinx=0\)

\(\Leftrightarrow2sinx-1-cos3x\left(2sinx-1\right)=0\)

\(\Leftrightarrow\left(2sinx-1\right)\left(1-cos3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cos3x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)

\(sin4x-2cos2x.cosx=0\)

\(\Leftrightarrow2sin2x.cos2x-2cos2x.cosx=0\)

\(\Leftrightarrow cos2x\left(sin2x-cosx\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\\sin2x-cosx=0\left(1\right)\end{matrix}\right.\)

Xét (1)

\(\Leftrightarrow sin2x=cosx=sin\left(\frac{\pi}{2}-x\right)\)

\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-x+k2\pi\\2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\left(cosx+sin2x\right).sin2x=0\)

\(\Leftrightarrow\left(cosx+2sinx.cosx\right).2sinx.cosx=0\)

\(\Leftrightarrow\left(1+2sinx\right)sinx.cos^2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}1+2sinx=0\\sinx.cosx=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\frac{1}{2}\\sin2x=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\\2x=k\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\\x=\frac{k\pi}{2}\end{matrix}\right.\)

\(cosx+cos3x+cos2x+cos4x=0\)

\(\Leftrightarrow2cos2x.cosx+2cos3x.cosx=0\)

\(\Leftrightarrow cosx\left(cos2x+cos3x\right)=0\)

\(\Leftrightarrow2cosx.cos\frac{5x}{2}.cos\frac{x}{2}=0\)

\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos\frac{x}{2}=0\\cos\frac{5x}{2}=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\\frac{x}{2}=\frac{\pi}{2}+k\pi\\\frac{5x}{2}=\frac{\pi}{2}+k\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pi+k2\pi\\x=\frac{\pi}{5}+\frac{k2\pi}{5}\end{matrix}\right.\)

Vậy nghiệm của phương trình là:

\(\begin{array}{l}a)\;sin2x + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) =  - cos3x\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = cos\left( {\pi  - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 2x = \pi  - 3x + k2\pi \\\frac{\pi }{2} - 2x =  - \pi  + 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{{3\pi }}{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow \frac{1}{2}\;sin2x = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow sin2x = \frac{{\sqrt 2 }}{2} = sin\left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{4} + k2\pi \\2x = \pi  - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{8} + k\pi \\x = \frac{{3\pi }}{8} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}c)\;sinx + sin2x = 0\\ \Leftrightarrow sinx =  - sin2x\\ \Leftrightarrow sinx = sin( - 2x)\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2x + k2\pi \\x = \pi  + 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x =  - \pi  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

@Nguyễn Việt Lâm giúp em với ạ

a/ \(4cos^3x-3cosx-4\left(2cos^2x-1\right)+3cosx-4=0\)

\(\Leftrightarrow4cos^3x-8cos^2x=0\)

\(\Leftrightarrow4cos^2x\left(cosx-2\right)=0\)

\(\Leftrightarrow cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)

\(0< \frac{\pi}{2}+k\pi< 14\Rightarrow-\frac{1}{2}< k< \frac{14-\frac{\pi}{2}}{\pi}\Rightarrow k=\left\{0;1;2;3\right\}\)

\(\Rightarrow x=\left\{\frac{\pi}{2};\frac{3\pi}{2};\frac{5\pi}{2};\frac{7\pi}{2}\right\}\)

b/ Bạn coi lại đề, cái ngoặc thứ 2 thiếu \(\left(2cos\left(???\right)+cosx\right)\)

c/ Bạn coi lại đề, có 2 số hạng \(cos2x\) xuất hiện ở vế trái, cấp 3 chắc ko ai cho kiểu vậy đâu, nếu đúng thế thì người ta cộng luôn thành \(2cos2x\) cho rồi

a: ĐKXĐ: sin 2x<>1

=>2x<>pi/2+k2pi

=>x<>pi/4+kpi

\(\dfrac{cos2x}{sin2x-1}=0\)

=>cos2x=0

=>2x=pi/2+kpi

=>x=pi/4+kpi/2

Kết hợp ĐKXĐ, ta được:

x=3/4pi+k2pi hoặc x=7/4pi+k2pi

b: cos(sinx)=1

=>sin x=kpi

=>sin x=0

=>x=kpi

c: \(2\cdot sin^2x-1+cos3x=0\)

=>cos3x+cos2x=0

=>cos3x=-cos2x=-sin(pi/2-2x)=sin(2x-pi/2)

=>cos3x=cos(pi/2-2x+pi/2)=cos(pi-2x)

=>3x=pi-2x+k2pi hoặc 3x=-pi+2x+k2pi

=>x=-pi+k2pi hoặc x=pi/5+k2pi/5

e: cos3x=-cos7x

=>cos3x=cos(pi-7x)

=>3x=pi-7x+k2pi hoặc 3x=-pi+7x+k2pi

=>x=pi/10+kpi/5 hoặc x=pi/4-kpi/2