cho hình thang cân ABCD , có AB//CD . Gọi M ,N tương ứng là trung điểm của AB và CD . Chứng tỏ rằng hình thang cân ABCD có 1 trục đối xứng là MN

Những câu hỏi liên quan
hình thang cân ABCD (AB // CD), đường trung bình MN của hình thang cân. Gọi E và F lần lượt là trung điểm cảu AB và CD. Xác định điểm đối xứng của các điểm A, N, C qua EF
cho hình thang cân ABCD, có AD//CD. Gọi M, N tương ứng là trung điểm của AB và CD. Chứng tỏ rằng hình thang cân ABCD có một trục đối xứng là MN
Xét tam giác AMD và tam giác BMC
góc DAM=góc MBC(hình thang cân)
cạnh AD=BC(hình thang cân)
AM=MB(trung điểm)
=>tam giác AMD=tam giác BMC
=>MD=MC
=>tam giác DMN=tam giác CMN
=>góc DNM=góc CNM
Mà góc DNM+góc CNM=180
=>góc DNM=góc CNM=90 độ=>D,C đối xứng với nhau qua M(1)
Do AB//CD
=>góc AMN=góc BMN=90 độ=>A,B đối xứng với nhau qua N(2)
Từ (1)(2)=>MN là 1 trục đối xứng của hình thang ABCD
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD (AB // CD). Gọi O là giao điểm của 2 đường chéo, I là trung điểm của hình thang. Chứng minh OI là trục đối xứng của hình thang
Vẽ hình thang cân ABCD (AB // CD), đường trung bình MN của hình thang cân. Gọi E và F lần lượt là trung điểm cảu AB và CD. Xác định điểm đối xứng của các điểm A, N, C qua EF
Trong không gian cho hình thang cân ABCD có AB//CD, AB a,CD 2a,AD a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB = a,CD = 2a,AD = a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
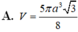
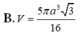
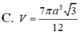
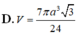
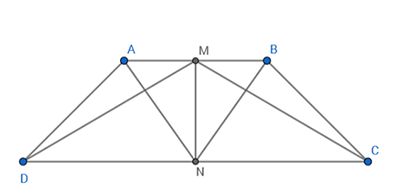
Trong không gian cho hình thang cân ABCD có AB//CD, ABa, CD2a, ADa. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K. A.
V
5
πa
3
3
8
B.
V
5
πa
3...
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB=a, CD=2a, AD=a. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
A. V = 5 πa 3 3 8
B. V = 5 πa 3 3 16
C. V = 7 πa 3 3 12
D. V = 7 πa 3 3 12
cho hình thang cân ABCD ( AB // CD). Gọi H, K lần lượt là trung điểm của AB và CD. Chứng minh rằng A đối xứng với B qua HK
Xét ΔADK và ΔBCK có
AD=BC
\(\widehat{D}=\widehat{C}\)
DK=CK
Do đó: ΔADK=ΔBCK
Suy ra: KA=KB
hay K nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra KH là đường trung trực của AB
hay A và B đối xứng nhau qua HK
Đúng 1
Bình luận (0)
Bài 1: Vẽ hình thang ABCD (AB//CD) đường trung bình MN của hình thang cân, gọi E,F lần lượt là trung điểm của AB và CD. Xác định điểm đối xứng với các điểm A,N,C qua EF.
cho hinh thang cân ABCD có AB song song với CD gọi M , N tương ứng là trung điểm của AB và CD . chứng minh rằng hình thang cân ABCD có một trục đối xứng là MN

Xét tam giác AMD và tam giác BMC
góc DAM=góc MBC(hình thang cân)
cạnh AD=BC(hình thang cân)
AM=MB(trung điểm)
=>tam giác AMD=tam giác BMC
=>MD=MC
=>tam giác DMN=tam giác CMN
=>góc DNM=góc CNM
Mà góc DNM+góc CNM=180
=>góc DNM=góc CNM=90 độ=>D,C đối xứng với nhau qua M(1)
Do AB//CD
=>góc AMN=góc BMN=90 độ=>A,B đối xứng với nhau qua N(2)
Từ (1)(2)=>MN là 1 trục đối xứng của hình thang ABCD
Đúng 0
Bình luận (0)















