giúp e 1 trong 5 bài này ạ(Hết thì càng tốt ạ)

Những câu hỏi liên quan
Các Anh/Chị ơi giải giúp e bài này càng nhanh càng tốt ạ ,e cảm ơn ạ!
Bài 18. Tìm một phân số biết rằng nếu thêm vào tử số 26 đv thì PS có giá trị bằng 1 biết trung bình cộng của MS và TS là 120?
(Ai trả lời nhanh e kêu mấy bạn lớp e tích đúng ạ, e muốn có lời giải chi tiết ạ)
Hiệu của mẫu số và tử số là 26
Tổng của tử số và mẫu số là:
120 × 2 = 240
Tử số là:
(240 - 26) : 2 = 107
Mẫu số là:
107 + 26 = 133
Phân số cần tìm là 107/133
Đúng 1
Bình luận (0)
Chị Vũ Linh ơi chị có thể giúp em trả lời câu hỏi này và có lời giải chi tiết dc k ạ?
Cho phân số a/b. Rút gọn a/b ta được phân số là 3/7. Nếu đem tử số của phân số đã cho cộng với 25 và giữ nguyên mẫu số thì được phân số mới .Sau khi rút gọn phân số mới thì được 2/3. Tìm phân số đã cho.
Mong chị giúp em
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
mọi người làm giúp e bài 1 nhé đc bài 2 thì càng tốt ạ. cảm ơn mọi người
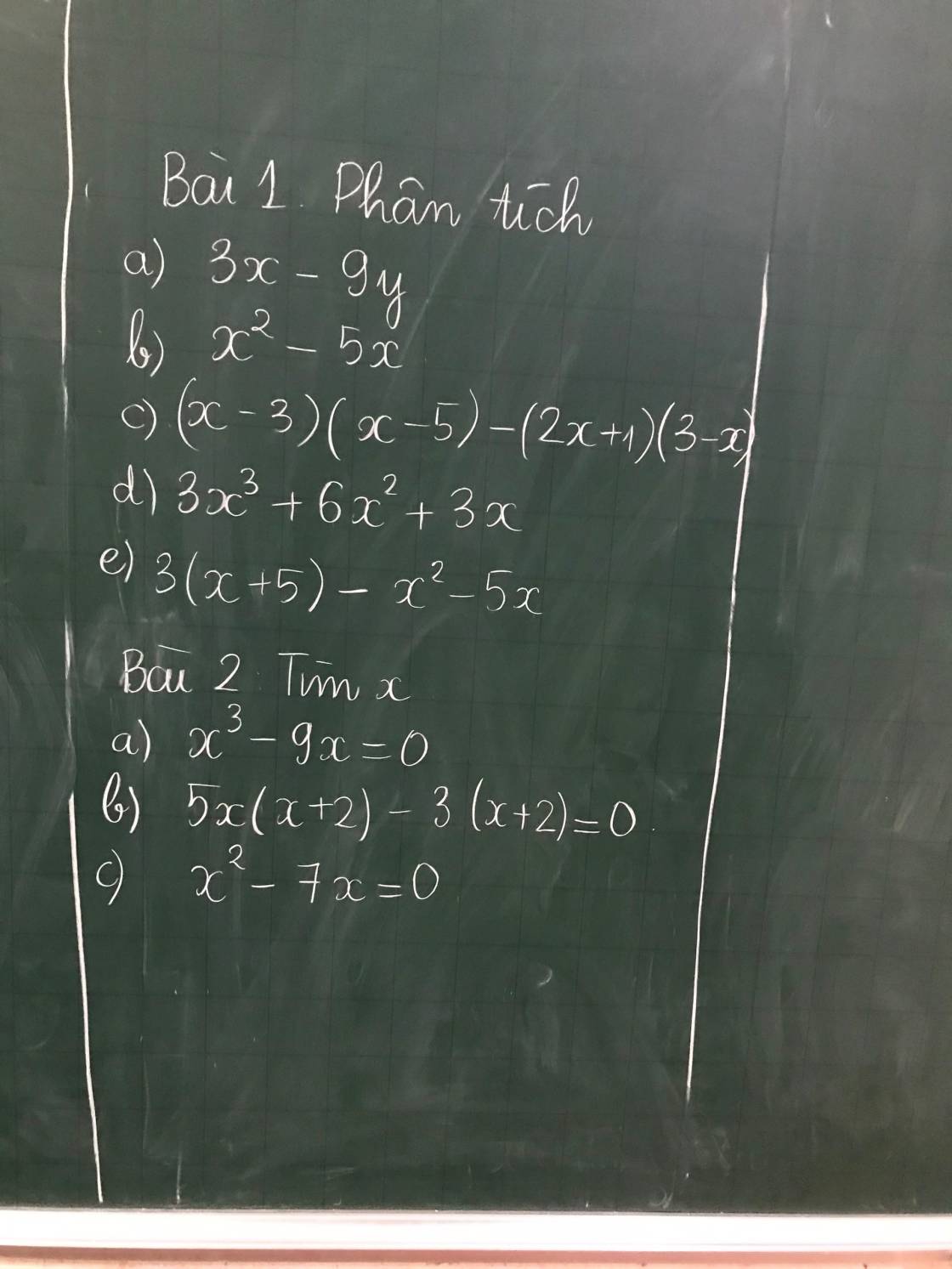
\(Bài.1:\\ a,3x-9y=3\left(x-3y\right)\\ b,x^2-5x=x\left(x-5\right)\\ c,\left(x-3\right)\left(x-5\right)-\left(2x+1\right)\left(3-x\right)=\left(x-3\right)\left(x-5\right)+\left(x-3\right)\left(2x+1\right)\\ =\left(x-3\right)\left(x-5+2x+1\right)=\left(x-3\right)\left(3x-4\right)\\ d,3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\\ e,3\left(x+5\right)-x^2-5x=3\left(x+5\right)-x\left(x+5\right)\\ =\left(x+5\right)\left(3-x\right)\)
Đúng 3
Bình luận (0)
\(Bài.2:\\ a,x^3-9x=0\\ \Leftrightarrow x.\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\\ b,5x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-2\end{matrix}\right.\\ c,x^2-7x=0\\ \Leftrightarrow x\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
Đúng 2
Bình luận (0)

hãy giúp mình bài 9c, 10, 11, 12, 13. Mọi người làm đc bài nào thì giúp mình bài ý không cần làm hết cả 4 đâu ạ 1 bài thôi cũng đc mà cả 4 thì càng tốt ạ cảm ơn mọi người
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
Đúng 0
Bình luận (0)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
Đúng 0
Bình luận (0)
13 b) \(\left(a+b\right)\left(ab+1\right)\ge2\sqrt{ab}.2\sqrt{ab}=4ab\)
Dấu = xảy ra khi a=b=1
Đúng 0
Bình luận (0)
mn ơi giúp em bài này với
ko cần hình vẽ cũng dc ạ ( có thì càng tốt mà ko có cũng ko sao ạ)
a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật
Đúng 1
Bình luận (1)
Mn ơi giúp e với
Làm giúp e 2 câu này ạ
Làm đc 1 câu cũng đc ạ mà 2 càng tốt ạ=))
Mong mn giúp e sớm tại e sắp thi giữa kì r :((
Câu 2
\((1) MnO_2 + 4HCl \to MnCl_2 + Cl_2 + 2H_2O\\ (2) Cl_2 + H_2 \xrightarrow{as} 2HCl\\ (3) 3Cl_2 + 2Fe \xrightarrow{t^o} 2FeCl_3\\ (4) 2FeCl_3 + Fe \to 3FeCl_2\\ (5) 2NaOH + Cl_2 \to NaCl + NaClO + H_2O\)
Đúng 2
Bình luận (0)
\((1) 4Al + 3O_2 \xrightarrow{t^o} 2Al_2O_3\\ (2) 2Fe + 3Cl_2 \xrightarrow{t^o} 2FeCl_3\\ (3) C + O_2 \xrightarrow{t^o} CO_2\\ (4) 2KMnO_4 \xrightarrow{t^o} K_2MnO_4 + MnO_2 + O_2\\ (5) 4P + 5O_2 \xrightarrow{t^o} 2P_2O_5\\ (6) 2KClO_3 \xrightarrow{t^o} 2KCl + 3O_2\\ (7) Fe + H_2SO_4 \to FeSO_4 + H_2\\ (8) Cu + 2H_2SO_4 \to CuSO_4 + SO_2 + 2H_2O\\ (9) 2Fe + 6H_2SO_4 \to Fe_2(SO_4)_3 + 3SO_2 + 6H_2O\\ (10) 2Al + 6H_2SO_4 \to Al_2(SO_4)_3 + 3SO_2 + 6H_2O\)
Đúng 1
Bình luận (0)

Giúp mình bài này với ạ, chi tiết càng tốt ạ <3
a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Đúng 2
Bình luận (0)
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).
Đúng 1
Bình luận (0)
Mọi người giúp em mấy câu này với ạ!! Một vài câu cũng được mà làm hết thì càng tốt

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
Đúng 1
Bình luận (0)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
7.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-\left(x+1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^2\left(x+3\right)}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{3}{1+1+1}=1\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+3\right)=3\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
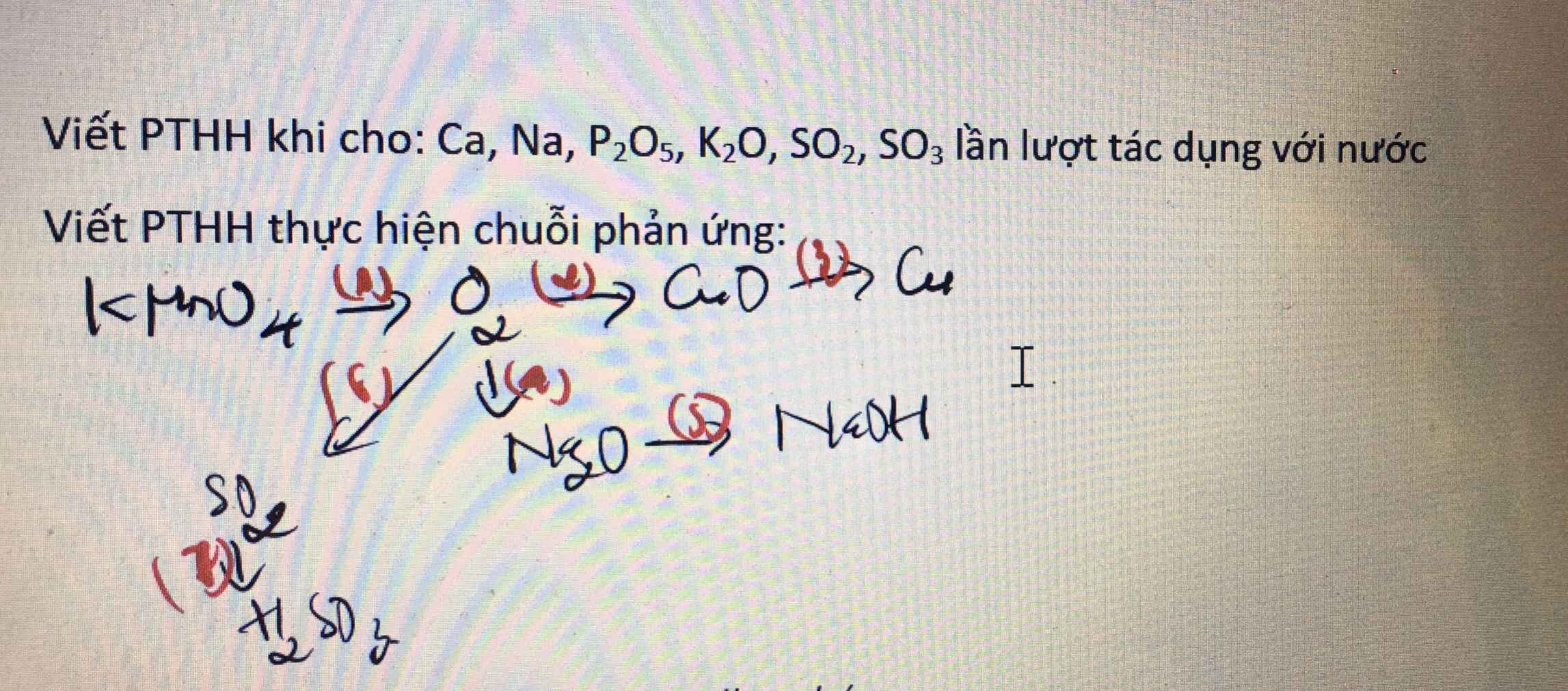
Giúp mình làm bài này vs mọi người!! Càng nhanh càng tốt ạ
1.
\(Ca+2H_2O\rightarrow Ca\left(OH\right)_2+H_2\)
\(2Na+2H_2O\rightarrow2NaOH+H_2\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
\(K_2O+H_2O\rightarrow2KOH\)
\(SO_2+H_2O\rightarrow H_2SO_3\)
\(SO_3+H_2O\rightarrow H_2SO_4\)
2.
(1)\(2KMnO_4\rightarrow\left(t^o\right)K_2MnO_4+MnO_2+O_2\)
(2)\(2Cu+O_2\rightarrow\left(t^o\right)2CuO\)
(3)\(CuO+H_2\rightarrow\left(t^o\right)Cu+H_2O\)
(4)\(4Na+O_2\rightarrow\left(t^o\right)2Na_2O\)
(5)\(Na_2O+H_2O\rightarrow2NaOH\)
(6)\(S+O_2\rightarrow\left(t^o\right)SO_2\)
(7)\(SO_2+H_2O\rightarrow H_2SO_3\)
Đúng 6
Bình luận (0)
(1) 2KMnO4 --to--> K2MnO4 + MnO2 + O2
(2) 2Cu + O2 --to--> 2CuO
(3) CuO + CO --to--> Cu + CO2
(4) 4Na + O2 --to--> 2Na2O
(5) Na2O + H2O ---> 2NaOH
(6) S + O2 --to--> SO2
(7) SO2 + H2O ---> H2SO3
Đúng 2
Bình luận (1)
mọi người giúp em bài này càng nhiều cách càng tốt ạ, em cảm ơn ^^

Quy đổi hỗn hợp X thành \(\left\{{}\begin{matrix}Ba\\Na\\O\end{matrix}\right.\) với nBa = x mol, nNa = y mol và nO = z mol
nH2 = 1,12 :22,4 = 0,05 mol
\(\left\{{}\begin{matrix}Ba\\Na\\O\end{matrix}\right.\) + H2O → \(\left\{{}\begin{matrix}Ba\left(OH\right)_2\\NaOH\end{matrix}\right.\) + H2
Ta có nBa(OH)2 = 20,52: 171 = 0,12 mol
Bảo toàn nguyên tố Ba => x = 0,12 mol
Áp dụng ĐLBT electron và BTKL ta có \(\left\{{}\begin{matrix}y+0,12.2=2z+0,05.2\\0,12.137+23y+16z=21,9\end{matrix}\right.\)
=> y = 0,14 và z = 0,14
a) BTKL => nNaOH = nNa = 0,14 mol
b) nOH- trong dung dịch Y = 0,12.2 +0,14 = 0,38 mol
nCO2 = 6,72:22,4 = 0,3 mol
Ta có \(\dfrac{nOH^-}{nCO_2}\) = 1,26 => tạo 2 muối HCO3- và CO32-
CO2 + OH- → HCO3-
0,3 0,38(dư) 0,3
OH- + HCO3- → CO32- + H2O
0,08 0,3 0,08
CO32- + Ba2+ → BaCO3
0,08 0,12 ---> 0,08
Vậy mBaCO3 = m kết tủa = 0,08.197 = 15,76 gam
Đúng 1
Bình luận (0)
Cách 2
\(\left[{}\begin{matrix}Na\\Ba\\Na_2O\\BaO\end{matrix}\right.\) + H2O → \(\left\{{}\begin{matrix}Ba\left(OH\right)_2\\NaOH\left(xmol\right)\end{matrix}\right.\) + H2
Tổng số mol H sau phản ứng = 2nBa(OH)2 + nNaOH + 0,05.2 = (0,34 +x) mol
=> nH2O phản ứng = 0,17 + 0,5x mol
Áp dụng ĐLBT khối lượng => 21,9 + (0,17 + 0,5x).18 = 20,52 + 40x + 0,05.2
=> x = 0,14
Đến đây em giải tiếp tương tự cách 1
Đúng 1
Bình luận (0)
























