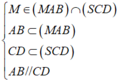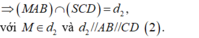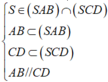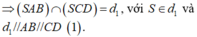Cho hình chóp S.ABCD đáy là hình thang có đáy lớn là AB, đáy nhỏ là CD. Lấy 1 điểm bất kì trên SD . Tìm giao tuyến của
( SAC ) giao ( MBC)

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. Tìm giao tuyến của các mặt phẳng: d 2 = S C D ∩ M A B
Phần II: Tự luận
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. Tìm giao tuyến của các mặt phẳng: d 1 = S A B ∩ S C D
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AD. M, N lần lượt là trung điểm SB, SC và P là điểm nằm trên đoạn SD sao cho PD = 2SP. a) Tìm giao tuyến của mp(SAB) và mp(SCD); giao tuyến của mp (SAC) và mp (SBD). b) Tìm giao tuyến của mp (SAD) và mp(SBC) c) Tìm giao điểm E của CD và mp (MNP); giao F của MP và (ABCD). CỨU EM VỚI QUÝ DỊ ƠI!!!
a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)
Đúng 1
Bình luận (0)
Cho hình Chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SAB), (SAB)và (SCD)
b. Trên SC lấy điểm M tùy ý. Tìm giao điểm K của SD và mp (ABM)
c. Tìm thiết diện của hình chóp với mặt phẳng (ABM)
giúp mình với
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB song song CD. Lấy điểm M thuộc SB. Tìm giao tuyến của (ADM) và (SAC)
Gọi O là giao của AC với BD trong mp(ABCD)
Trong mp(SBD), gọi E là giao của SO với DM
\(E\in SO\subset\left(SAC\right)\)
\(E\in DM\subset\left(ADM\right)\)
=>E thuộc (SAC) giao (ADM)
mà \(A\in\left(SAC\right)\cap\left(ADM\right)\)
nên \(\left(SAC\right)\cap\left(ADM\right)=EA\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang với
A
B
/
/
C
D
. Gọi I là giao điểm của AC và BD. Trên cạnh SB lấy điểm M. Giao tuyến của hai mặt phẳng (ADM) và (SAC) là A. SI B. AE (E là giao điểm của DM và SI). C. DM D. DE (E là giao điểm của DM và SI).
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang với A B / / C D . Gọi I là giao điểm của AC và BD. Trên cạnh SB lấy điểm M. Giao tuyến của hai mặt phẳng (ADM) và (SAC) là
A. SI
B. AE (E là giao điểm của DM và SI).
C. DM
D. DE (E là giao điểm của DM và SI).
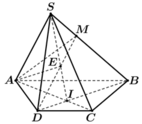
Ta có A là điểm chung thứ nhất.
Gọi 
=> E là điểm chung thứ hai.
Vậy AE là giao tuyến của (ADM) và (SAC)
Chọn B.
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AD. Gọi H,K lần lượt là trung điểm SB, SD, I = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
a: \(I\in BD\subset\left(SBD\right)\)
\(I\in AC\subset\left(SAC\right)\)
Do đó: \(I\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SI\)
b: Gọi K là giao của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
c: AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: \(\left(SAD\right)\cap\left(SBC\right)=xy\), xy đi qua S và xy//AD//BC
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy là hình thang (AB//CD). a) Tim giao tuyến của (SAD)và(SCB) b)Tìm giao tuyến của (SAB)và(SCD) c) Trên SD, SC lấy 2 điểm M, N .Tìm MN giao (SAO). GIÚP TÔI VỚI
c: Chọn mp(SDC) có chứa MN
Ta có: \(SC\subset\left(SDC\right);SC\subset\left(SAC\right)\)
Do đó: \(\left(SDC\right)\cap\left(SAC\right)=SC \)
Ta có: \(MN\cap SC=\left\{N\right\}\)
=>N là giao điểm của MN và mp(SAC)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.
a) Tìm giao điểm của MN và mặt phẳng (SAC).
b) Tìm thiết diện của hình chóp với mặt phẳng (NBC). Thiết diện đó là hình gì?
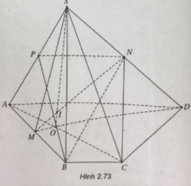
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.
Đúng 0
Bình luận (0)