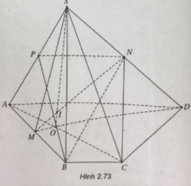
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
cho hình chóp s.abcd đáy abcd là hình thang AD//BC, O là giao điểm của ac và bd gọi M,N lần lượt là trung điểm SA,SD.xác định thiết diện hình chóp cắt bởi mặt phẳng omn
cho hình chóp s.abcd có đáy là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạng SA,SC, và G là trọng tâm của △ABC
a) tìm giao tuyến của hai mặt phẳng (SAC) và (SBD)
b) tìm giao điểm BC và mặt phẳng (GMN)
c) xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (GMN)
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, lần lượt là hai trung điểm của AB, CD. Gọi (P) là mặt phẳng đi qua MN và cắt mặt bên (SBC) theo một giao tuyến. Thiết diện của (P) và hình chóp là:
A. Hình bình hành.
A. B. Hình chữ nhật.
C. hình thang.
D. Hình vuông.
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, lần lượt là hai trung điểm của AB, CD. Gọi (P) là mặt phẳng đi qua MN và cắt mặt bên (SBC) theo một giao tuyến. Thiết diện của (P) và hình chóp là:
A. Hình bình hành.
A. B. Hình chữ nhật.
C. hình thang.
D. Hình vuông.
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AD. Gọi H,K lần lượt là trung điểm SB, SD, I = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình bình hành; M, N lần lượt là trung điểm của (SB, SD) a) Chứng minh đường thẳng BD song song với mặt phẳng (AMN) b) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD). Tìm giao điểm của đường thẳng MN và mặt phẳng (SAC)
