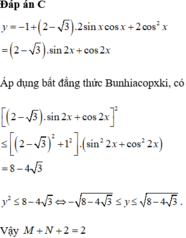a)\(-1\le sinx\le1\)

\(\Leftrightarrow1\ge-sinx\ge-1\)

\(\Leftrightarrow4\ge3-sinx\ge2\) \(\Leftrightarrow16\ge\left(3-sinx\right)^2\ge4\)\(\Leftrightarrow17\ge\left(3-sinx\right)^2+1\ge5\)

\(\Leftrightarrow17\ge y\ge5\)

\(y_{min}=5\Leftrightarrow sinx=1\)\(\Leftrightarrow\)\(x=\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)

\(y_{max}=17\Leftrightarrow\)\(sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)

b)\(y=\left(sin^2x+cos^2x\right)^2-2.sinx^2cos^2x\)\(=1-\dfrac{1}{2}.sin^22x\)

Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{1}{2}.sin^22x\ge-\dfrac{1}{2}\)

\(\Leftrightarrow1\ge1-\dfrac{1}{2}.sin^22x\ge\dfrac{1}{2}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{2}\)

\(y_{min}=\dfrac{1}{2}\Leftrightarrow sin^22x=1\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}sin2x=-1\\sin2x=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)

\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)

c)\(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1-3sin^2x.cos^2x=1-\dfrac{3}{4}.sin^22x\)

Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{3}{4}.sin^22x\ge-\dfrac{3}{4}\)

\(\Leftrightarrow1\ge1-\dfrac{3}{4}.sin^22x\ge\dfrac{1}{4}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{4}\)

​\(y_{min}=\dfrac{1}{4}\Leftrightarrow sin^22x=1\)​\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)​​

\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)

Vậy...

a, Đặt \(t=sinx\left(t\in\left[-1;1\right]\right)\)

\(y=f\left(t\right)=\left(3-t\right)^2+1=t^2-6t+10\)

\(\Rightarrow min=min\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(1\right)=5\)

\(\Rightarrow max=max\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(-1\right)=17\)

b, \(y=sin^4x+cos^4x=1-2sin^2x.cos^2x=1-\dfrac{1}{2}sin^22x\)
Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)

\(y=f\left(t\right)=1-\dfrac{1}{2}t^2\)

\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{2}\)

\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)

c, \(y=sin^6x+cos^6x\)

\(=sin^4x+cos^4x-sin^2x.cos^2x\)

\(=1-3sin^2x.cos^2x\)

\(=1-\dfrac{3}{4}sin^22x\)

Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)

\(y=f\left(t\right)=1-\dfrac{3}{4}t^2\)

\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{4}\)

\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)

\(P=sin^4x-cos^4x=\left(sin^2x+cos^2x\right)\left(sin^2x-cos^2x\right)\)

\(\Rightarrow P=-\left(cos^2x-sin^2x\right)=-cos2x\)

Do \(-1\le cos2x\le1\Rightarrow-1\le P\le1\)

\(\Rightarrow\left\{{}\begin{matrix}P_{min}=-1\Rightarrow x=k\pi\\P_{max}=1\Rightarrow x=\frac{\pi}{2}+k\pi\end{matrix}\right.\)

b/

\(P=sin^6x+cos^6x=\left(sin^2x+cos^2x\right)\left(sin^4x+cos^4x-sin^2x.cos^2x\right)\)

\(P=sin^4x+cos^4x+2sin^2x.cos^2x-3sin^2x.cos^2x\)

\(P=\left(sin^2x+cos^2x\right)^2-\frac{3}{4}\left(2sinx.cosx\right)^2\)

\(P=1-\frac{3}{4}sin^22x\)

Do \(0\le sin^22x\le1\Rightarrow\frac{1}{4}\le P\le1\)

\(\Rightarrow\left\{{}\begin{matrix}P_{min}=\frac{1}{4}\Rightarrow x=\frac{k\pi}{4}\\P_{max}=1\Rightarrow x=\frac{k\pi}{2}\end{matrix}\right.\)

c/

\(P=1-2\left|cos3x\right|\)

Do \(0\le\left|cos3x\right|\le1\Rightarrow-1\le P\le1\)

\(\Rightarrow\left\{{}\begin{matrix}P_{min}=-1\Rightarrow x=\frac{k\pi}{3}\\P_{max}=1\Rightarrow x=\frac{k\pi}{6}\end{matrix}\right.\)

\(A=\cos^4x+2\sin^2x.\cos^2x\left(\sin^2x+\cos^2x\right)+\sin^4x+1\)

\(=\cos^4x+2\sin^2x.\cos^2x+\sin^4x+1\)

\(=\left(\sin^2x+\cos^2x\right)^2+1=1+1=2\)

\(0< =sin^2x< =1\)

=>\(-2< =sin^2x-2< =-1\)

=>\(sin^2x-2< 0\)

\(0< =cos^2x< =1\)

=>\(-2< =cos^2x-2< =-1\)

\(\Leftrightarrow cos^2x-2< 0\)

\(\sqrt{sin^4x+4cos^2x}+\sqrt{cos^4x+4\cdot sin^2x}\)

\(=\sqrt{sin^4x+4\left(1-sin^2x\right)}+\sqrt{cos^4x+4\cdot\left(1-cos^2x\right)}\)

\(=\sqrt{sin^4x-4sin^xx+4}+\sqrt{cos^4x-4\cdot cos^2x+4}\)

\(=\sqrt{\left(sin^2x-2\right)^2}+\sqrt{\left(cos^2x-2\right)^2}\)

\(=\left|sin^2x-2\right|+\left|cos^2x-2\right|\)

\(=2-sin^2x+2-cos^2x\)

\(=4-\left(sin^2x+cos^2x\right)=4-1=3\)

\(sinx+cosx=\sqrt{2}\)

\(\Leftrightarrow\left(sinx+cosx\right)^2=2\)

\(\Leftrightarrow sin^2x+cos^2x+2.sinx.cosx=2\)

\(\Leftrightarrow1+2.sinx.cosx=2\)

\(\Leftrightarrow2.sinx.cosx=1\)

Khi đó \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2.sinx.cosx=1^2-1=0\)