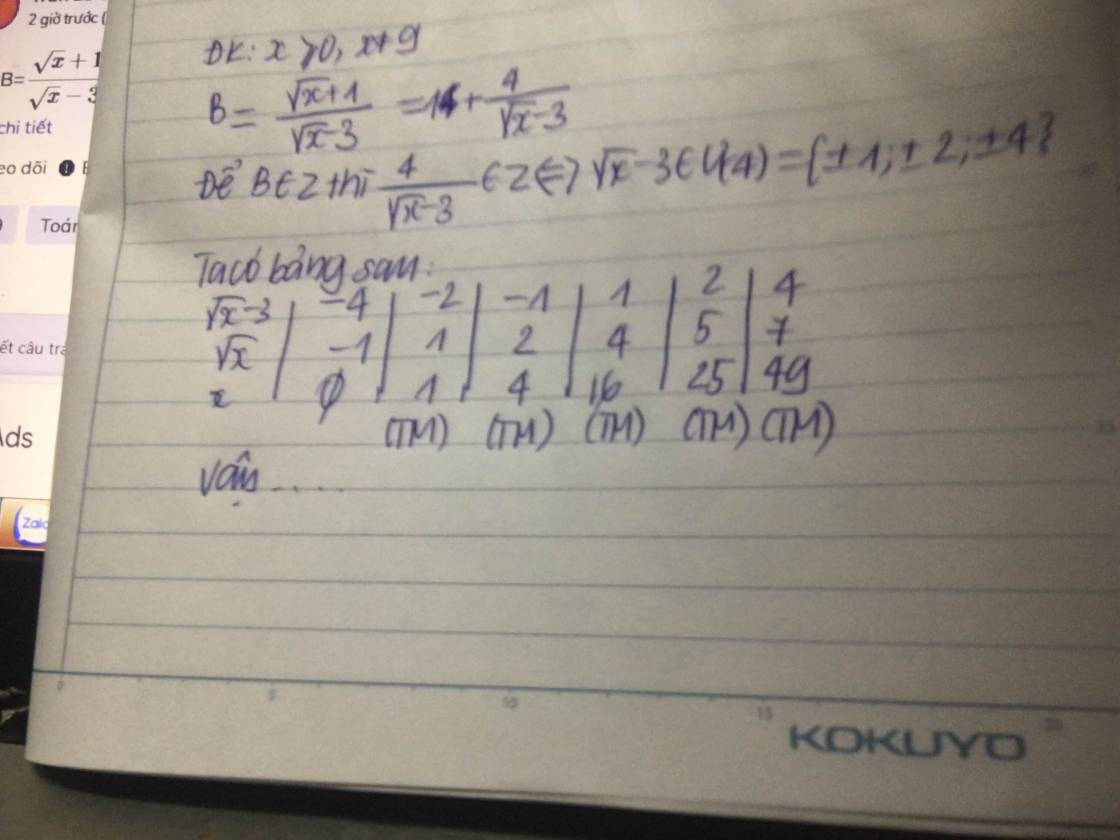Biểu thức gì vậy bạn?

tìm các giá trị nguyên của x để biểu thức P=A.B  nhận giá trị nguyên

\(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\left(x\ge0;x\ne9\right)=\dfrac{\sqrt{x}+3-2}{\sqrt{x}+3}=1-\dfrac{2}{\sqrt{x}+3}\)

Để \(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\in Z\Leftrightarrow\dfrac{2}{\sqrt{x}+3}\in Z\)

\(\Leftrightarrow2⋮\sqrt{x}+3\\ \Leftrightarrow\sqrt{x}+3\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-5;-4;-2;-1\right\}\\ \Leftrightarrow x\in\left\{1;4;16;25\right\}\)

Vậy \(x\in\left\{1;4;16;25\right\}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\in Z\)

Tick plz

ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\\sqrt{x}+3\ne0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne-3\left(loại\right)\end{matrix}\right.\)\(\Rightarrow x\ge0\)

\(x\in Z\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\in Z\Rightarrow\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}+3\right)\)

\(\Rightarrow\left(\sqrt{x}+3-2\right)⋮\left(\sqrt{x}+3\right)\)

Vì \(\Rightarrow\left(\sqrt{x}+3\right)⋮\left(\sqrt{x}+3\right)\)

\(\Rightarrow2⋮\left(\sqrt{x}+3\right)\Rightarrow\sqrt{x}+3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)

Ta có bảng:

Vậy không có x nguyên thỏa mãn đề bài

\(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}=\dfrac{\sqrt{x}+3}{\sqrt{x}+3}-\dfrac{2}{\sqrt{x}+3}=1-\dfrac{2}{\sqrt{x}+3}\)

Để \(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\in Z\) thì \(2⋮\sqrt{x}+3\Rightarrow\sqrt{x}+3\in\) Ư(2)\(=\left\{1;-1;2;-2\right\}\)

Vì \(\sqrt{x}\ge0\Rightarrow x\in\varnothing\)

a: \(P=\left(\dfrac{2+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

b: Để P nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)

\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)

hay \(x\in\left\{0;4;9\right\}\)

\(P=A\cdot B\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{2\sqrt{x}+6+x-3\sqrt{x}+3-5\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)}\cdot\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+3\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}-3\right)^2}=\dfrac{2\sqrt{x}}{\sqrt{x}+3}\)

Để P nguyên thì 

\(2\sqrt{x}⋮\sqrt{x}+3\)

\(\Leftrightarrow2\sqrt{x}+6-6⋮\sqrt{x}+3\)

=>\(\sqrt{x}+3\inƯ\left(-6\right)\)

=>\(\sqrt{x}+3\in\left\{3;6\right\}\)

=>\(\sqrt{x}\in\left\{0;3\right\}\)

=>\(x\in\left\{0;9\right\}\)

Kết hợp ĐKXĐ, ta được: x=0

Để M là số nguyên thì \(12\sqrt{x}+5⋮3\sqrt{x}-1\)

=>\(12\sqrt{x}-4+9⋮3\sqrt{x}-1\)

=>\(3\sqrt{x}-1\in\left\{1;-1;3;-3;9;-9\right\}\)

=>\(3\sqrt{x}\in\left\{2;0;4;10\right\}\)

=>\(\sqrt{x}\in\left\{0;\dfrac{2}{3};\dfrac{4}{3};\dfrac{10}{3}\right\}\)

mà x là số chính phương

nên x=0

\(M=\dfrac{12\sqrt{x}+5}{3\sqrt{x}-1}\)

\(M=\dfrac{12\sqrt{x}-4+9}{3\sqrt{x}-1}\)

\(M=\dfrac{4\left(3\sqrt{x}-1\right)+9}{3\sqrt{x}-1}\)

\(M=\dfrac{4\left(3\sqrt{x}-1\right)}{3\sqrt{x}-1}+\dfrac{9}{3\sqrt{x}-1}\)

\(M=4+\dfrac{9}{3\sqrt{x}-1}\)

M nguyên khi: 

\(9\) ⋮ \(3\sqrt{x}-1\)

Mà: \(3\sqrt{x}-1\ge-1\)

\(\Rightarrow3\sqrt{x}-1\in\left\{1;-1;3;9\right\}\)

\(\Rightarrow\sqrt{x}\in\left\{\dfrac{2}{3};0;\dfrac{4}{3};\dfrac{10}{3}\right\}\)

\(\Rightarrow x\in\left\{\dfrac{4}{9};0;\dfrac{16}{9};\dfrac{100}{9}\right\}\)

Mà: x là số chính phương nên:

x = 0

ĐKXĐ: x>=0

Để A là số nguyên thì \(\sqrt{x}+13⋮\sqrt{x}+5\)

=>\(\sqrt{x}+5+8⋮\sqrt{x}+5\)

=>\(\sqrt{x}+5\inƯ\left(8\right)\)

mà \(\sqrt{x}+5>=5\)

nên \(\sqrt{x}+5=8\)

=>x=9

ĐK: \(x\ge0\) 

Để \(\dfrac{\sqrt{x}+13}{\sqrt{x}+5}\) có giá trị nguyên 

Mà:  \(\dfrac{\sqrt{x}+13}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5+8}{\sqrt{x}+5}\)

\(=\dfrac{\sqrt{x}+5}{\sqrt{x}+5}+\dfrac{8}{\sqrt{x}+5}=1+\dfrac{8}{\sqrt{x}+5}\)

Vậy:  \(8\) ⋮ \(\sqrt{x}+5\)

\(\Rightarrow\sqrt{x}+5\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)

Mà: \(\sqrt{x}+5\ge5\)

\(\Rightarrow\sqrt{x}+5\in\left\{8\right\}\)

\(\Rightarrow x=9\left(tm\right)\)

ĐKXĐ: \(x>0;x\ne9\)

\(P=\left(\dfrac{x+7}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}-\dfrac{4\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\right)\left(\dfrac{\sqrt{x}+6}{\sqrt{x}}\right)\)

\(=\left(\dfrac{x+7-4\sqrt{x}-4+\sqrt{x}-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\right)\left(\dfrac{\sqrt{x}+6}{\sqrt{x}}\right)\)

\(=\left(\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\right).\left(\dfrac{\sqrt{x}+6}{\sqrt{x}}\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}.\dfrac{\left(\sqrt{x}+6\right)}{\sqrt{x}}\)

\(=\dfrac{\sqrt{x}+6}{\sqrt{x}+1}\)

b.

Ta có \(P=\dfrac{\sqrt{x}+1+5}{\sqrt{x}+1}=1+\dfrac{5}{\sqrt{x}+1}\)

Do \(\sqrt{x}+1>0\Rightarrow\dfrac{5}{\sqrt{x}+1}>0\Rightarrow P>1\)

\(P=\dfrac{6\left(\sqrt{x}+1\right)-5\sqrt{x}}{\sqrt{x}+1}=6-\dfrac{5\sqrt{x}}{\sqrt{x}+1}\)

Do \(\left\{{}\begin{matrix}5\sqrt{x}>0\\\sqrt{x}+1>0\end{matrix}\right.\) ;\(\forall x>0\Rightarrow\dfrac{5\sqrt{x}}{\sqrt{x}+1}>0\)

\(\Rightarrow P< 6\Rightarrow1< P< 6\)

Mà P nguyên \(\Rightarrow P=\left\{2;3;4;5\right\}\)

- Để \(P=2\Rightarrow\dfrac{\sqrt{x}+6}{\sqrt{x}+1}=2\Rightarrow\sqrt{x}+6=2\sqrt{x}+2\Rightarrow x=16\)

- Để \(P=3\Rightarrow\dfrac{\sqrt{x}+6}{\sqrt{x}+1}=3\Rightarrow\sqrt{x}+6=3\sqrt{x}+3\Rightarrow\sqrt{x}=\dfrac{3}{2}\Rightarrow x=\dfrac{9}{4}\)

- Để \(P=4\Rightarrow\dfrac{\sqrt{x}+6}{\sqrt{x}+1}=4\Rightarrow\sqrt{x}+6=4\sqrt{x}+4\Rightarrow\sqrt{x}=\dfrac{2}{3}\Rightarrow x=\dfrac{4}{9}\)

- Để \(P=5\Rightarrow\dfrac{\sqrt{x}+6}{\sqrt{x}+1}=5\Rightarrow\sqrt{x}+6=5\sqrt{x}+5\Rightarrow\sqrt{x}=\dfrac{1}{4}\Rightarrow x=\dfrac{1}{16}\)