cho ba điểm (1;2)B (1;2)C (3;m) tìm m để A,B,C thẳng hàng

Những câu hỏi liên quan
Cho hai bộ ba điểm: M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1). Hỏi bộ nào có ba điểm thẳng hàng?
Ta có: MN → = (−5; 2; 0) và MP → = (−10; 4; 0). Hai vecto MN → và MP → thỏa mãn điều kiện: MN → = k MP → với k = k/2 nên ba điểm M, N, P thẳng hàng.
Đúng 0
Bình luận (0)
Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).
a) Chứng minh ba điểm A, B, G không thẳng hàng.
b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
Đúng 0
Bình luận (0)
Cho hai bộ ba điểm: A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1). Hỏi bộ nào có ba điểm thẳng hàng?
Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó 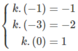
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
Đúng 0
Bình luận (0)
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C. A.
N
2
;
-
4
7
;
0
B. N(2;0;0) C.
N
2
;
7
4...
Đọc tiếp
Cho ba điểm A(1;1;1), B(-1;-1;0), C(3;1;-1). Tìm tọa độ điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
A. N 2 ; - 4 7 ; 0
B. N(2;0;0)
C. N 2 ; 7 4 ; 0
D. N(0;0;2)
Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.
Đúng 0
Bình luận (0)
Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d:
x
-
3
y
-
1
z
2
Tìm tập hợp những điểm cách đều ba điểm A, B, C.
Đọc tiếp
Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: x - 3 = y - 1 = z 2
Tìm tập hợp những điểm cách đều ba điểm A, B, C.
Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 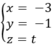
Đúng 0
Bình luận (0)
Cho ba điểm A(3;5),B(-1;-7),C(2;-1). Chứng minh ba điểm A,B,C thẳng hàng
\(\overrightarrow{AB}=\left(-4;-12\right)\)
\(\overrightarrow{AC}=\left(-1;-6\right)\)
Vì -4/-1<>-12/-6
nên A,B,C ko thẳng hàng
Đúng 0
Bình luận (0)
BÀI 1: Cho tam giác ABC. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 1/4AB; AE=1/2AC. DE cắt đường thẳng BC tại F. CM: CF = 1/2BC BÀI 2: Cho tam giác ABC. Điểm D thuộc tia đối của tia BA sao cho BD=BA, điểm M là trung điểm của BC. Gọi K là giao điểm của DM và AC. CM: AK = 2KC Help me! Mình đang cần gấp ạ.!!!
Cho ba điểm A(1; 1), B(4;3) và C(0;- 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD= 2AB.
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { - 1; - 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} - 0;{y_D} - \left( { - 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Điểm D thuộc tia đối của tia BA sao cho BD = BA, điểm M là trung điểm của BC. Gọi K là giao điểm của DM với AC. Chứng minh rằng: MK= 1/4 DK
Kẻ BE//DK(E\(\in\)AK)
Xét ΔADK có
B là trung điểm của AD
BE//DK
Do đó: E là trung điểm của AK
=>AE=EK
Xét ΔADK có B,E lần lượt là trung điểm của AD,AK
nên BE là đường trung bình của ΔADK
=>\(BE=\dfrac{1}{2}DK\)
Xét ΔBEC có
M là trung điểm của CB
MK//BE
Do đó: K là trung điểm của CE
Xét ΔBEC có
M,K lần lượt là trung điểm của CB,CE
=>MK là đường trung bình của ΔBEC
=>\(MK=\dfrac{1}{2}BE=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot DK=\dfrac{1}{4}\cdot DK\)
Đúng 1
Bình luận (0)
Cho ba điểm A(0; 1), B(1; 2), C(-5; -4).
a)Viết phương trình đường thẳng d đi qua hai điểm A và B.
b) Chứng minh ba điểm A, B, C thẳng hàng.
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
Đúng 0
Bình luận (0)












