a) Nếu ABC là một tam giác cân thì ABC là tam giác đều

Đây là mệnh đề sai

b) Nếu ABC là một tam giác cân và có một góc bằng 60o thì ABC là một tam giác đều

Đây là mệnh đề đúng

(P⇒Q) đúng, (Q⇒P) sai

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.

b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.

c)

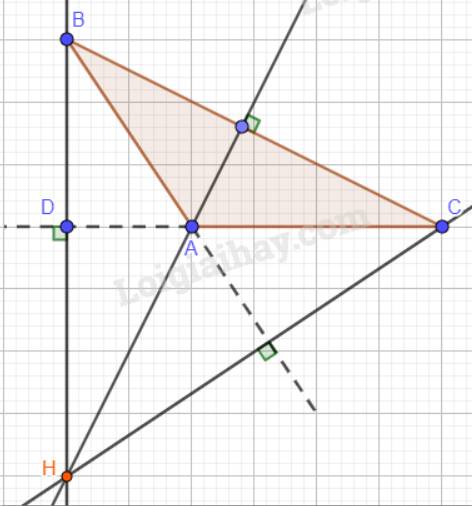
Nhận xét: H nằm ngoài tam giác ABC.

O cách đều 3 đỉnh của tam giác ABC

\( \Rightarrow \) \(OA = OB = OC\)

\( \Rightarrow \) \(\Delta OAB\) cân tại O.

Giả sử O là trung điểm BC

\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)

 \(\Delta OAC\) cân tại O 

\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)

Xét tam giác ABC có

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)

Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

4 cách phát biểu mệnh đề \(P \Leftrightarrow Q\):

“Tam giác ABC cân tương đương nó có hai đường cao bằng nhau”

“Tam giác ABC cân là điều kiện cần và đủ để nó có hai đường cao bằng nhau”

“Tam giác ABC cân khi và chỉ khi nó có hai đường cao bằng nhau”

“Tam giác ABC cân nếu và chỉ nếu nó có hai đường cao bằng nhau”

Xét tam giác ACJ vuông tại J:

\(AC^2=CJ^2+AJ^2\left(pytago\right)\)

\(\Rightarrow AJ=\sqrt{AC^2-CJ^2}=\sqrt{6^2-4,8^2}=3,6\left(cm\right)\)

Áp dụng HTL:

\(AC^2=AJ.AB\)

\(\Rightarrow AB=\dfrac{AC^2}{AJ}=\dfrac{6^2}{3,6}=10\left(cm\right)\)

Ta có: \(S_{ABC}=\dfrac{1}{2}CJ.AB=\dfrac{1}{2}.4,8.10=24\left(cm^2\right)\)

Câu c đổi lại thành trên tia đối tia NM ạ

Làm chắc câu d mà Tam giác ABC cần có thêm đk gì để tứ giác AECM là  hình thoi là đc nha

a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân

=> Loại

b: Gọi giao điểm của BH và AC là K

=> BK\(\perp\)AC tại K

Ta có: ΔABK vuông tại K

nên \(\widehat{ABK}+\widehat{BAK}=90^0\)

hay \(\widehat{BAC}=60^0\)

Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)

nên ΔABC đều

Đáp án B

 Áp dụng công thức tính diện tích tam giác S = p . r  trong đó p là nửa chu vi và r là bán kính đường tròn nội tiếp tam giác

Đặt  A B = A C = a , B C = b a , b > 0

Ta có: S A B C = p . r = p .1 = p = a + a + b 2 = a + b 2

Kẻ đường cao AH ta có: b 2 = a sin A 2 ⇒ S A B C = a + a sin A 2

Ta lại có S A B C = 1 2 a 2 sin A = a + a sin A 2 = a 1 + sin A 2

  ⇒ 1 2 a sin A = 1 + sin A 2 ⇔ a = 2 1 + sin A 2 sin A

⇒ S A B C = 2 1 + sin A 2 2 sin A 0 < A < π

Dùng M O D E 7 tìm GTNN của hàm số trên ta nhận được:

 Xấp xỉ