Cho ΔABC ⊥ A. Kẻ phân giác BE (E ∈ AC); EH ⊥ BC (H ∈ BC). Cho AB = 6cm, AC = 8cm. Tính BC và khoảng cách từ I đến 3 cạnh của ΔABC

Những câu hỏi liên quan
Bài 1 Cho ΔABC có AB 1/2AC. Gọi M là trung điểm của BC. Kẻ Ax là phân giác góc ngoài tại đỉnh A của ΔABC. Qua M kẻ MH ⊥ Ax (H∈Ax). Tia MH cắt AB tại E và cắt AC tại F. a) CMR: AEAFb) Qua B kẻ tia By// AC, By cắt MH tại I. CMR: BEBIc) CMR: BECFd) CMR: CFBFBài 2 Cho ΔABC có ABAC và đường phân giác AD (D∈BC). Trên tia AC lấy điểm E sao cho AEAB.a) CMR: BDDEb) Gọi K là giao điểm của AB và ED. CMR: ΔDBK Δ DECc) ΔABC cần có thêm điều kiện gì để điểm D cách đều 3 cạnh của ΔAKC
Đọc tiếp
Bài 1 Cho ΔABC có AB< 1/2AC. Gọi M là trung điểm của BC. Kẻ Ax là phân giác góc ngoài tại đỉnh A của ΔABC. Qua M kẻ MH ⊥ Ax (H∈Ax). Tia MH cắt AB tại E và cắt AC tại F.
a) CMR: AE=AF
b) Qua B kẻ tia By// AC, By cắt MH tại I. CMR: BE=BI
c) CMR: BE=CF
d) CMR: CF>BF
Bài 2 Cho ΔABC có AB<AC và đường phân giác AD (D∈BC). Trên tia AC lấy điểm E sao cho AE=AB.
a) CMR: BD=DE
b) Gọi K là giao điểm của AB và ED. CMR: ΔDBK= Δ DEC
c) ΔABC cần có thêm điều kiện gì để điểm D cách đều 3 cạnh của ΔAKC
Cho ΔABC vuông tại A ( AB < AC ), đường cao AH ( H ϵ BC ).
1. Chứng minh: ΔHBA đồng dạng ΔABC và BA.BA=BH.BC.
2. Kẻ phân giác BE của góc ABC ( E ϵ AC ) , BE cát AH tại I .
Chứng minh : ΔHBI đồng dạng ΔABE .
3. Chứng minh : AI=AE
1.Xét ΔHBA và ΔABC có:
góc AHB=góc BAC=90o
Góc B chung
=> ΔABC đồng dạng ΔHBA (g.g)
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)\(\Rightarrow BA.BA=BH.BC\)
2. Xét ΔHBI và ΔABE có:
góc ABE=IBH (Vì BE là tia phân giác của góc B, I nằm trên BE)
góc BAE=góc IHB=90o
=>ΔHBI đồng dạng ΔABE (g.g)
Đúng 1
Bình luận (1)
Cho ΔABC vuông tại A, phân giác BE (E ∈ AC). Kẻ EH ⊥ BC tại H. Chứng minh rằng:
a) EB là phân giác của AEH. b) BE là trung trực của AH.
c) ΔKEC cân (K là giao điểm của AB và EH). d) AE < EC.
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: \(\widehat{AEB}=\widehat{HEB}\)
hay EB là tia phân giác của \(\widehat{AEH}\)
b: Ta có: ΔBAE=ΔBHE
nên BA=BH và EA=EH
Ta có: BA=BH
nên B nằm trên đường trung trực của AH\(\left(1\right)\)
Ta có: EA=EH
nên E nằm trên đường trung trực của AH\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BE là đường trung trực của AH
Đúng 1
Bình luận (0)
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
Xét ΔEKC có EK=EC
nên ΔEKC cân tại E
d: Ta có: EA=EH
mà EH<EC
nên EA<EC
Đúng 1
Bình luận (0)
cho ΔABC cân tại A, ∠A < 90 độ, kẻ BE ⊥ AC (E ϵ AC ),CD⊥ AB (D ϵ AB). gọi I là giao điểm của BE và CD
a, CM : AD=AE
b, CM :AI là tia phân giác của ∠BAC
C,CM: BI > CE
a) Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}\) chung
Do đó: ΔAEB=ΔADC(cạnh huyền-góc nhọn)
Suy ra: AE=AD(Hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Bài 1: Cho ΔABC vuông tại A, phân giác BE của góc B (E ∈ AC). Từ E kẻ ED ⊥ BC (D thuộc BC). Đường thẳng BE cắt tia BA tại F a) Chứng minh rằng ΔEAB ΔEDB b) Chứng minh rằng EC EF ( Vẽ hình, viết giả thiết kết luận )Bài 2: Cho ΔABC có AB AC. Gọi M là trung điểm của BC a) Chứng minh ΔABM ΔACM b) Chứng minh AM ⊥ BC c) Chứng minh AM là phân giác của góc BAC ( Vẽ hình, viết giả thiết kết luận )
Đọc tiếp
Bài 1: Cho ΔABC vuông tại A, phân giác BE của góc B (E ∈ AC). Từ E kẻ ED ⊥ BC (D thuộc BC). Đường thẳng BE cắt tia BA tại F
a) Chứng minh rằng ΔEAB = ΔEDB
b) Chứng minh rằng EC = EF
( Vẽ hình, viết giả thiết kết luận )
Bài 2: Cho ΔABC có AB = AC. Gọi M là trung điểm của BC
a) Chứng minh ΔABM = ΔACM
b) Chứng minh AM ⊥ BC
c) Chứng minh AM là phân giác của góc BAC
( Vẽ hình, viết giả thiết kết luận )
Bài 2:

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của \(\widehat{BAC}\)
Bài 1:
a: XétΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: ΔBAE=ΔBDE
=>EA=ED
Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔEAF=ΔEDC
=>EF=EC
Đúng 1
Bình luận (0)
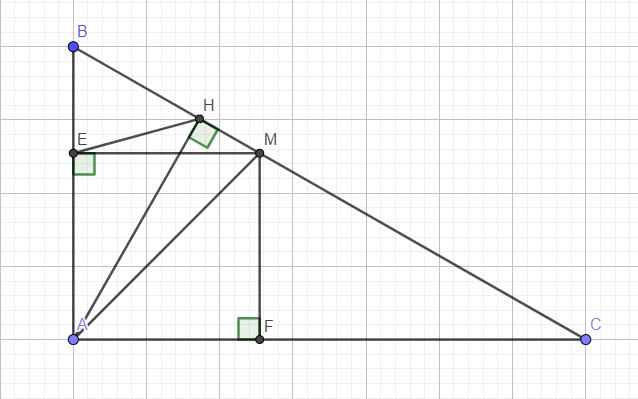
Cho ΔABC vuông tại A có AB<AC. Kẻ đường cao AH, phân giác AM, kẻ ME⊥AB, MF⊥AC.
a) CMR: BE.BA=BH.BM, HE là tia phân giác góc AHB
b) CM:\(\dfrac{BE}{CF}=\dfrac{HB}{HC}\)
a: Xét ΔBEM vuông tại E và ΔBHA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔBEM∼ΔBHA
Suy ra: \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\)
hay \(BE\cdot BA=BH\cdot BM\)
Đúng 3
Bình luận (0)
Tứ giác AEHM nội tiếp (E và H cùng nhìn AM dưới 1 góc vuông)
\(\Rightarrow\widehat{AHE}=\widehat{AME}=45^0\) (AEMF là hv nên AME=45 độ)
\(\Rightarrow\widehat{BHE}=\widehat{AHB}-\widehat{AHE}=45^0=\widehat{AHE}\)
\(\Rightarrow HE\) là phân giác AHB
Cũng do AEHM nội tiếp \(\Rightarrow\widehat{EAH}=\widehat{EMH}\)
Mà \(\widehat{EMH}=\widehat{FCH}\) (đồng vị) \(\Rightarrow\widehat{EAH}=\widehat{FCH}\) (1)
Tứ giác AHMF nội tiếp (H và F cùng nhìn AM dưới 1 góc vuông)
\(\Rightarrow\widehat{MHF}=\widehat{MAF}=45^0\Rightarrow\widehat{MHF}=\widehat{AHE}\) (2)
(1);(2) \(\Rightarrow\Delta AEH\sim\Delta CFH\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{AE}=\dfrac{CH}{CF}\) (3)
Áp dụng định lý phân giác cho tam giác ABH: \(\dfrac{AH}{AE}=\dfrac{BH}{BE}\) (4)
(3);(4) \(\Rightarrow\dfrac{CH}{CF}=\dfrac{BH}{BE}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Cho ΔABC vuông tại A có AB<AC. Kẻ đường cao AH, phân giác AM, kẻ ME⊥AB, MF⊥AC.
a) CMR: BE.BA=BH.BM, HE là tia phân giác góc AHB
b) CM:\(\dfrac{BE}{CF}=\dfrac{HB}{HC}\)
Cho ΔABC vuông tại A, vẽ BD là tia phân giác góc ABC (D∈AC). Trên cạnh BC, lấy điểm E sao cho AB=BE, từ A kẻ AH vuông góc với BC (H∈ BC). Chứng minh rằng góc BAH = góc ACB.
Xét tam giác vuông ABHGóc HAB+ góc HBA=90độ(1)
Xét tam giác vuông ABC: góc ABC + góc ACB=90 độ(2)
Từ (1),(2)=> góc HAB = góc HCA
Đúng 0
Bình luận (0)
Bài 1:Cho ΔABC có ABAc,kẻ AD là tia phân giác của góc BAC (DϵBC) a,SO sánh góc B và góc C.Từ đó chứng minh góc ADB góc ADC. b,Trên cạnh AC lấy điểm AEAD.Chứng minh góc AED góc ABD.Bài 2:Cho ΔABC có ACAB,phân giác AD gọi E là một điêmt nằm giữa A và D(E khác A và D).Trên cạnh AC lấy điểm F sao cho AFAc a,Chứng minh EBEF b,Chứng minh FCEC-EB c,Chứng minh AC-ABEC-EB
Đọc tiếp
Bài 1:Cho ΔABC có AB<Ac,kẻ AD là tia phân giác của góc BAC (DϵBC)
a,SO sánh góc B và góc C.Từ đó chứng minh góc ADB< góc ADC.
b,Trên cạnh AC lấy điểm AE=AD.Chứng minh góc AED= góc ABD.
Bài 2:Cho ΔABC có AC>AB,phân giác AD gọi E là một điêmt nằm giữa A và D(E khác A và D).Trên cạnh AC lấy điểm F sao cho AF=Ac
a,Chứng minh EB=EF
b,Chứng minh FC>EC-EB
c,Chứng minh AC-AB>EC-EB
1:
a: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC
b: Sửa đề; AE=AB
Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>góc ABD=góc AED
Đúng 0
Bình luận (0)
Cho ΔABC có ∠A=50°,∠C=110°. Kẻ tia phân giác BE của góc B (E ∈ AC), vẽ tia Ax sao cho ∠BAx=20° sao cho tia Ax cắt BE tại F. Gọi I là trung điểm của AF, EI kéo dài cắt AB tại K. CK cắt BE tại M.
a, CMR: ∆AEF cân
b, CMR: ∆CEB=∆KEB