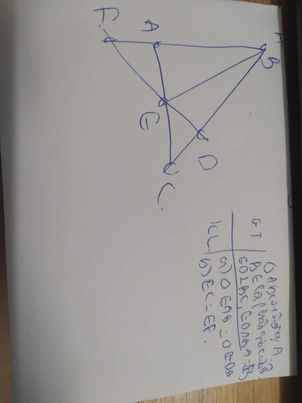
Bài 1: Cho ΔABC vuông tại A, phân giác BE của góc B (E ∈ AC). Từ E kẻ ED ⊥ BC (D thuộc BC). Đường thẳng BE cắt tia BA tại F
a) Chứng minh rằng ΔEAB = ΔEDB
b) Chứng minh rằng EC = EF
( Vẽ hình, viết giả thiết kết luận )
Bài 2: Cho ΔABC có AB = AC. Gọi M là trung điểm của BC
a) Chứng minh ΔABM = ΔACM
b) Chứng minh AM ⊥ BC
c) Chứng minh AM là phân giác của góc BAC
( Vẽ hình, viết giả thiết kết luận )
Bài 2:

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của \(\widehat{BAC}\)
Bài 1:
a: XétΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: ΔBAE=ΔBDE
=>EA=ED
Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔEAF=ΔEDC
=>EF=EC