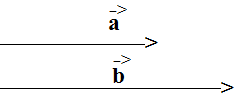chứng minh : \(\left(\overrightarrow{a};\overrightarrow{b}\right)=0^o\Rightarrow\overrightarrow{a},\overrightarrow{b}\) cùng hướng
\(\left(\overrightarrow{a};\overrightarrow{b}\right)=90^o\Rightarrow\overrightarrow{a}\perp\overrightarrow{b}\)
\(\left(\overrightarrow{a};\overrightarrow{b}\right)=180^o\Rightarrow\overrightarrow{a},\overrightarrow{b}\) đối nhau
sáng mai mình cần rùi, mong các bn giúp đỡ.................