cho tam giác đều ABC nội tiếp đường tròn tâm 0. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM+AN=AB. Chứng minh OM=ON và góc MON=120
BÀI 6: Khái niệm về phép dời hình và hai hình bằng nhau
Cho tam giác abc. vẽ về phía ngoài tam giác một hình chữ nhật BCDE. Các đường cao xuất phát từ D và E lần lượt vuông góc với AB và AC và cắt nhau tại I. Chứng minh rằng AI và BC vuông góc với nhau.
Các bạn giúp mình bài này nhé! Mình cảm ơn các bạn nhiều!
Cho tứ giác lồi ABCD và 1 điểm M được xác định bởi vecto AB= vecto DM, góc CBM = góc CDM. C/m góc ACD = góc BCM.
Lấy điểm N sao cho tứ giác CDMN là hình bình hành =>
Ta có:\(\overrightarrow{AB}=\overrightarrow{DM}=\overrightarrow{CN}\)
Tứ giác BMCN có nên là tứ giác nội tiếp =>
(1) và (2)=> GOOD LUCK
Đúng 0
Bình luận (0)
4. Trong mặt phẳng Oxy, cho đường thẳng d: x − 3y + 1 = 0 và điểm I(−3; 1).
(a) Tìm ảnh của điểm M(1; −2) qua phép đối xứng tâm I.
(b) Tìm ảnh của đường thẳng ∆: 2x + y − 1 = 0 qua phép đối xứng tâm I.
(c) Tìm ảnh của đường tròn (C): (x − 2)2 + (y + 3)2 = 9 qua phép đối xứng
mik mất gốc hình từ cấp 2 mong mọi người cho mik hỏi tại sao đoạn cuối lại suy ra đc thế mong mn giải thích hộ 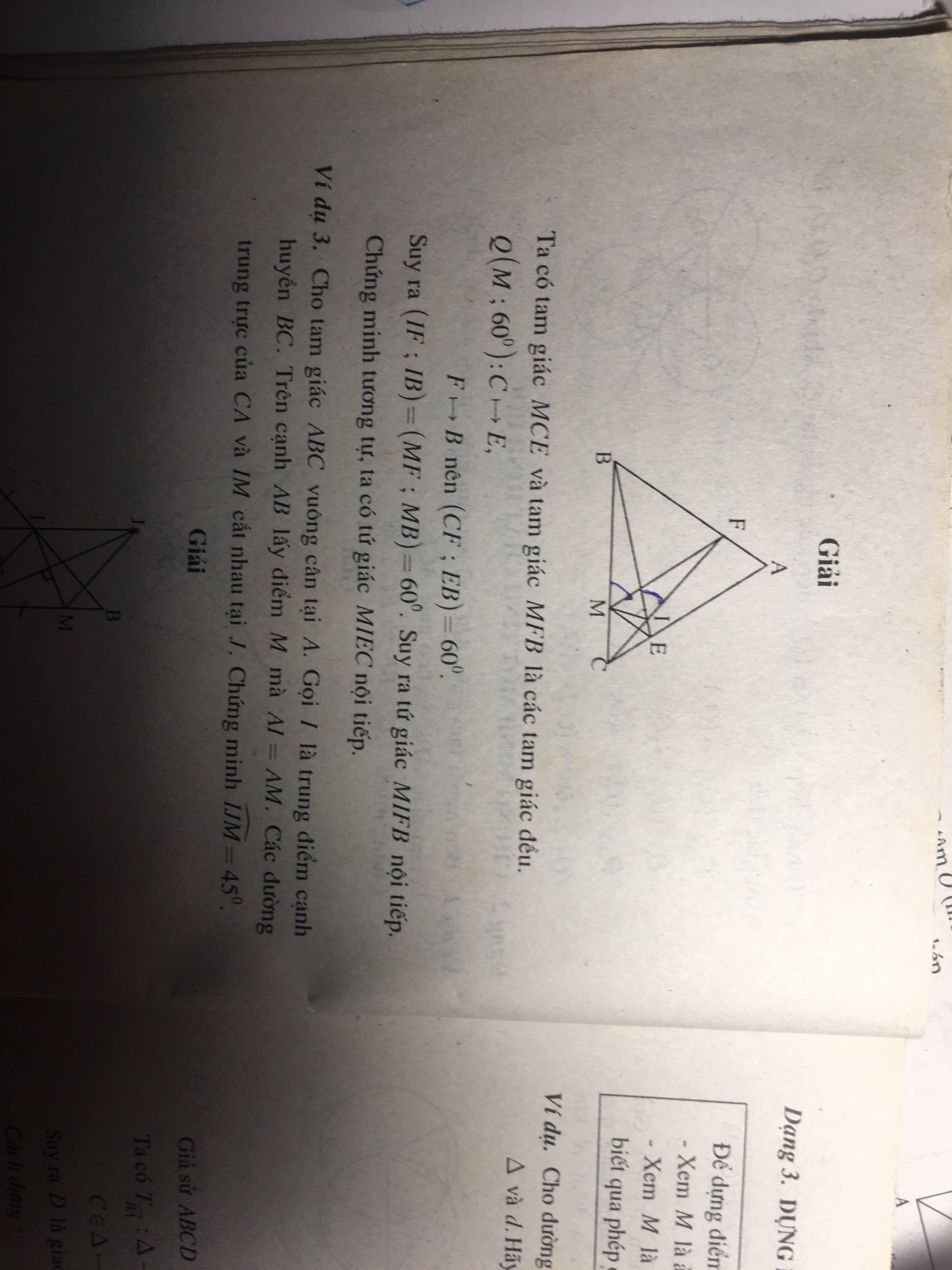
) Trong mặt phẳng tọa độ Oxy cho điểm M (3; 2) .Tìm ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v(1;5) và phép quay tâm O góc quay 900
\(T_{\overrightarrow{v}}\left(M\right)=M_1\Rightarrow\left\{{}\begin{matrix}x_{M1}=3+1=4\\y_{M1}=2+5=7\end{matrix}\right.\) \(\Rightarrow M_1\left(4;7\right)\)
\(Q_{\left(0;90^0\right)}\left(M_1\right)=M_2\Rightarrow\left\{{}\begin{matrix}x_{M2}=-y_{M1}=-7\\y_{M2}=x_{M1}=4\end{matrix}\right.\)
Vậy ảnh của điểm M qua 2 phép dời hình nói trên là \(M_2\left(-7;4\right)\)
Đúng 0
Bình luận (0)
Trong mp Oxy cho điểm A(1,2),đường thẳng d co pt:2x-3y+10 và véc tơv(-3,1)a)Tìm ảnh của A,(d) qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép tịnh tiến theo vb) tìm điểm M sao cho A là ảnh của M qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo vc) tìm điểm d’ sao cho d là ảnh của d’ qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
Đọc tiếp
Trong mp Oxy cho điểm A(1,2),đường thẳng d co pt:2x-3y+1=0 và véc tơ
v=(-3,1)
a)Tìm ảnh của A,(d) qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép tịnh tiến theo v
b) tìm điểm M sao cho A là ảnh của M qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
c) tìm điểm d’ sao cho d là ảnh của d’ qua phép dời hình có đc bằng cách thực hiện liên tiếp phép quay tâm O góc quay- 90 độ và phép tịnh tiến theo v
Cho tam giác ABC . Trên cạnh AC lấy 14 điểm phân biệt khác hai điểm A C, rồi nối chúng với B . Trên cạnh BC lấy 7 điểm phân biệt khác hai điểm B C, rồi nối chúng với A . Số tam giác đếm được trên hình khi này là k . Khi đó:
A. k =1981 . B. k = 1203 . C. k =1380 . D. k =147
















