Cho tam giác \(ABC\), biết \(DE//BC\) và \(AE = 6cm,EC = 3cm,DB = 2cm\) (Hình 1). Độ dài đoạn thẳng \(AD\) là
A. 4cm.
B. 3 cm.
C. 5cm.
D. 3,5 cm.
Bài tập cuối chương VII
Bài 1 (SGK Chân trời sáng tạo trang 58)
Thảo luận (2)
Bài 2 (SGK Chân trời sáng tạo trang 58)
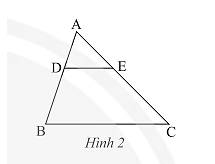
Cho tam giác \(ABC\), biết \(DE//BC\) (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\).
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
C. \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
D. \(\frac{{BD}}{{AB}} = \frac{{DE}}{{BC}}\).
Thảo luận (2)Hướng dẫn giải
Bài 3 (SGK Chân trời sáng tạo trang 58)
Cho Hình 3, biết \(AM = 3cm;MN = 4cm;AC = 9cm.\) Giá trị của biểu thức \(x - y\) là
A. 4.
B. -3.
C. 3.
D. -4
Thảo luận (2)Hướng dẫn giảiVì \(\left\{ \begin{array}{l}MN \bot MC\\BC \bot MC\end{array} \right. \Rightarrow MN//BC\) (quan hệ từ vuông góc đến song song).
Xét tam giác \(ABC\) có\(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AC}} \Leftrightarrow \frac{4}{x} = \frac{3}{9} \Rightarrow x = \frac{{4.9}}{3} = 12\).
Xét tam giác \(ABC\) vuông tại \(C\) ta có:
\(A{C^2} + B{C^2} = A{B^2}\) (định lí Py – ta – go)
\( \Leftrightarrow {9^2} + {12^2} = {y^2} \Rightarrow y = \sqrt {81 + 144} = 15\)
Do đó, \(x - y = 12 - 15 = - 3\)
(Trả lời bởi Hà Quang Minh)
Bài 4 (SGK Chân trời sáng tạo trang 58)
Cho tam giác \(MNP\) có \(MD\) là tia phân giác góc \(M\left( {D \in NP} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{DN}}{{MN}} = \frac{{DP}}{{MP}}\).
B. \(\frac{{DN}}{{MN}} = \frac{{MP}}{{DP}}\).
C. \(\frac{{DN}}{{MN}} = \frac{{MP}}{{DP}}\).
D. \(\frac{{MN}}{{MP}} = \frac{{DP}}{{DN}}\).
Thảo luận (2)Hướng dẫn giải
Bài 5 (SGK Chân trời sáng tạo trang 58)
Cho hai đoạn thẳng \(AB = 12cm\) và \(CD = 18cm\). Tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) là
A. \(\frac{4}{3}\).
B. \(\frac{3}{4}\).
C. \(\frac{2}{3}\).
D. \(\frac{3}{2}\).
Thảo luận (2)Hướng dẫn giải
Bài 6 (SGK Chân trời sáng tạo trang 58)
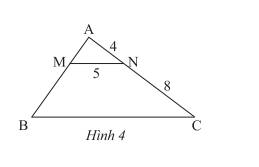
Cho Hình 4, biết \(MN//BC,AN = 4cm,NC = 8cm,MN = 5cm.\) Độ dài cạnh \(BC\)
A. 10cm.
B. 20cm.
C. 15cm.
D. 16cm.
Thảo luận (2)Hướng dẫn giải
Bài 7 (SGK Chân trời sáng tạo trang 59)
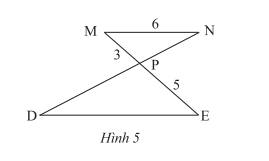
Cho Hình 5, biết \(MN//DE,MN = 6cm;MP = 3cm;PE = 5cm\). Độ dài đoạn thẳng \(DE\) là
A. 6cm.
B. 5cm.
C. 8cm.
D. 10cm.
Thảo luận (2)Hướng dẫn giải
Bài 8 (SGK Chân trời sáng tạo trang 59)
Cho \(\Delta ABC\), một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) lần lượt tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\) cắt \(AB\) tại \(F\). Biết \(AB = 25cm,AF = 9cm,EF = 12cm\), độ dài đoạn \(DC\) là
A. 25cm.
B. 20cm.
C. 15cm.
D. 12cm
Thảo luận (2)Hướng dẫn giải
Bài 9 (SGK Chân trời sáng tạo trang 59)
Cho \(\Delta ABC\) biết \(AM\) là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}\).
B. \(\frac{{AB}}{{MC}} = \frac{{BM}}{{AC}}\).
C. \(\frac{{AM}}{{MC}} = \frac{{AB}}{{AC}}\).
D. \(\frac{{BM}}{{MC}} = \frac{{AM}}{{AC}}\).
Thảo luận (2)Hướng dẫn giải
Bài 10 (SGK Chân trời sáng tạo trang 59)
Cho tam giác \(ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(AD = 13,5cm;DB = 4,5cm\). Tính tỉ số các khoảng cách từ điểm \(D\) và \(B\) đến đoạn thẳng \(AC\).
Thảo luận (2)Hướng dẫn giảikẻ DH và BG vuông góc AC
=>DH//BG
Xét ΔABG có DH//BG
nên AD/DB=AH/HG=3
=>AH=3HG
=>DH/BG=3/4
(Trả lời bởi Nguyễn Lê Phước Thịnh)