kẻ DH và BG vuông góc AC
=>DH//BG
Xét ΔABG có DH//BG
nên AD/DB=AH/HG=3
=>AH=3HG
=>DH/BG=3/4
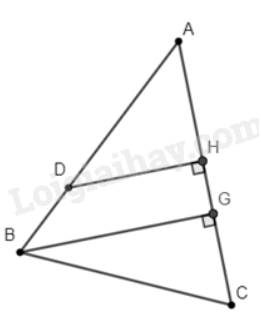
Gọi \(H;G\) lần lượt là hình chiếu vuông góc của \(D;B\)lên \(AC\).
Khi đó, khoảng cách từ \(D\) đến \(AC\) là \(DH\);khoảng cách từ \(B\) đến \(AC\) là \(BG\).
Ta có: \(AB = AD + BD = 13,5 + 4,5 = 18cm\)
Vì \(\left\{ \begin{array}{l}DH \bot AC\\BG \bot AC\end{array} \right. \Rightarrow DH//BG\)
Xét tam giác \(ABG\) có \(DH//BG\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{DH}}{{BG}} \Leftrightarrow \frac{{13,5}}{{18}} = \frac{{DH}}{{BG}} = \frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến đoạn thẳng \(AC\) là \(\frac{3}{4}\).