Cho Hình78, biết \(A{H^2} = BH.CH\). Chứng minh:
a) \(\Delta HAB \backsim \Delta HCA\)
b) Tam giác ABC vuông tại A.
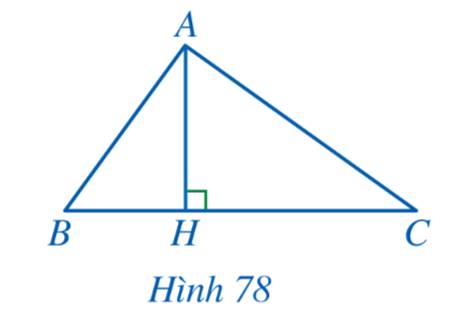
Cho Hình78, biết \(A{H^2} = BH.CH\). Chứng minh:
a) \(\Delta HAB \backsim \Delta HCA\)
b) Tam giác ABC vuông tại A.

Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thỏa mãn \(AB = 20m,{\rm{ }}AC = 0m,\;\,\,\widehat {BAC} = 135^\circ \)
Bạn Vy làm như sau: Vẽ tam giác A'B'C' có \(A'B' = 2cm,{\rm{ }}A'C' = 5cm,\;\widehat {B'A'C'} = 135^\circ \). Bạn Vy lấy thước đo khoảng cách giữa hai điểm B', C' và nhận được kết quả \(B'C'\; \approx \;6,6cm\). Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Thảo luận (1)Hướng dẫn giảiĐổi \(20m = 2000cm;\,\,50m = 5000cm\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{2}{{2000}} = \frac{1}{{1000}};\,\,\frac{{A'C'}}{{AC}} = \frac{5}{{5000}} = \frac{1}{{1000}}\)
\( \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {BAC} = \widehat {B'A'C'} = 135^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
Khi đó
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{{1000}}\\ \Rightarrow \frac{{6,6}}{{BC}} \approx \frac{1}{{1000}}\\ \Rightarrow BC \approx 6600cm = 66m\end{array}\)
Vì vậy Vy có thể kết luận rằng \(B'C'\; \approx \;6,6cm\).
(Trả lời bởi Hà Quang Minh)