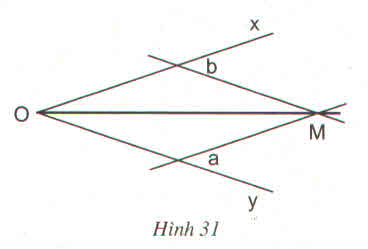
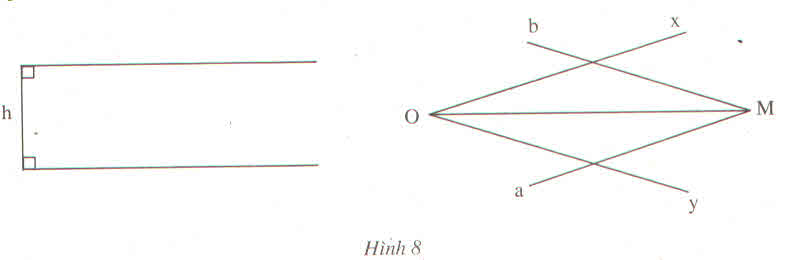
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề :
- Áp dụng một của thước và cạnh Ox, kẻ đường thẳng a theo lề kia
- Làm tương tự với đường thẳng b
- Gọi M là giao điểm của a và b, ta cso OM là tia phân giác của góc xOy
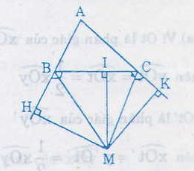
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy
(Gợi ý : Dựa vào bài tập 12 chứng minh các khoảng cách từ M đề Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai kề của chiếc thước) rồi áp dụng định lí 2)