Question

Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác hai góc ngoài \(B_1;C_1\) (H.32) nằm trên tia phân giác của góc A ?

Answer 1

Hướng dẫn :

Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC

Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC

( H ∈ AB, I ∈ BC, K ∈ AC)

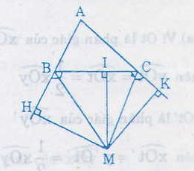
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)

MI = MK (Vì M thuộc phân giác của góc C ngoài)

Suy ra : MH = MK

=> M thuộc phân giác của góc

Answer 2

Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC

Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC

( H ∈ AB, I ∈ BC, K ∈ AC)

Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)

MI = MK (Vì M thuộc phân giác của góc C ngoài)

Suy ra : MH = MK

=> M thuộc phân giác của gócA