Tìm các số tự nhiên \(n\) thỏa mãn mỗi bất phương trình sau :
a) \(3\left(5-4n\right)+\left(27+2n\right)>0\)
b) \(\left(n+2\right)^2-\left(n-3\right)\left(n+3\right)\le40\)
Bài 4: Bất phương trình bậc nhất một ẩn.
Bài 64 (Sách bài tập - tập 2 - trang 58)
Thảo luận (1)
Bài 4.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 59)
Chọn đáp án đúng cho các khẳng định sau :
Bất phương trình \(x-2< 1\) tương đương với bất phương trình sau :
(A) \(x>3\) (B) \(x\le3\)
(C) \(x-1>2\) (D) \(x-1< 2\)
Thảo luận (1)Hướng dẫn giải
Bài 4.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 59)
Chọn đáp án đúng :
Bất phương bậc nhất \(2x-1>1\) có tập nghiệm biểu diễn bởi hình vẽ sau :
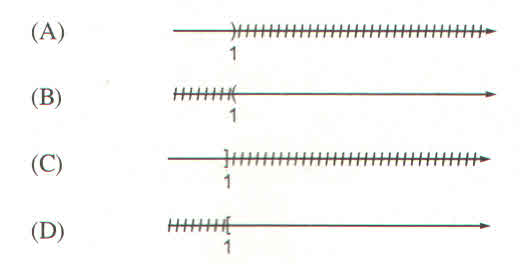
Thảo luận (1)Hướng dẫn giảiGiaỉ bất phương trình:
\(2x-1>1\\ < =>2x>1+1\\ =>2x>2\\ =>x>\dfrac{2}{2}\\ < =>x>1\)
Vậy: tập nghiệm của bất phương trình là S= \(\left\{x|x>1\right\}\)
Biễu diễn tập nghiệm:
Chọn hình B.
(Trả lời bởi Nguyễn Trần Thành Đạt)
Bài 4.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 59)
Với giá trị nào của \(m\) thì phương trình ẩn \(x\)
a) \(x-2=3m+4\) có nghiệm lớn hơn 3
b) \(3-2x=m-5\) có nghiệm nhỏ hơn -2
Thảo luận (2)Hướng dẫn giảia. \(x-2=3m+4\)
\(\Leftrightarrow x=3m+6\)
Để nghiệm của phương trình là \(x>3\) thì \(3m+6>3\Leftrightarrow3m>-3\Leftrightarrow m>-1\)
Vậy với \(m>-1\) thì nghiệm của phương trình \(x-2=3m+4\) lớn hơn 3.
b.\(3-2x=m-5\)
\(\Leftrightarrow-2x=m-8\)
\(\Leftrightarrow x=\dfrac{8-m}{2}\)
Để nghiệm của phương trình là \(x< -2\) thì \(\dfrac{8-m}{2}< -2\Leftrightarrow8-m< -4\Leftrightarrow m>12\)
Vậy với \(m>12\) thì phương trình \(3-2x=m-5\) có nghiệm nhỏ hơn -2
(Trả lời bởi Ha Hoang Vu Nhat)
Bài 4.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 59)
Chứng minh hai bất phương trình sau không tương đương :
a) \(2x+1>3\) và \(\left|x\right|>1\)
b) \(3x-9< 0\) và \(x^2< 9\)
Thảo luận (1)Hướng dẫn giải
