Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?
Bài 3: Phương trình mặt cầu
Khởi động (SGK Cánh Diều - Tập 2 - Trang 81)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều - Tập 2 - Trang 81)
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
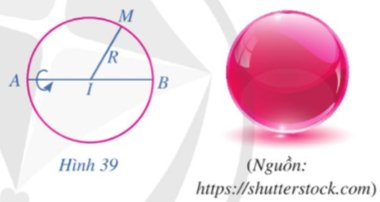
Thảo luận (1)Hướng dẫn giảiKhi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 1 (SGK Cánh Diều - Tập 2 - Trang 82)
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính đường kính của mặt cầu đó.
Thảo luận (1)Hướng dẫn giảiVì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 2 (SGK Cánh Diều - Tập 2 - Trang 83)
Cho hai điểm M(x; y; z) và I(a; b; c).
a) Viết công thức tính khoảng cách giữa hai điểm M và I.
b) Nêu mối liên hệ giữa x, y, và z để điểm M nằm trên mặt cầu tâm I bán kính R.
Thảo luận (1)Hướng dẫn giảia) Công thức tính khoảng cách giữa hai điểm M và I là: \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Để M nằm trên mặt cầu tâm I bán kính R thì \(IM = R\) hay \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 2 (SGK Cánh Diều - Tập 2 - Trang 83)
Tìm tâm và bán kính của mặt cầu có phương trình: x2 + (y + 5)2 + (z + 1)2 = 2
Thảo luận (1)Hướng dẫn giảiTa có: \({x^2} + {\left( {y + 5} \right)^2} + {\left( {z + 1} \right)^2} = 2 \Leftrightarrow {x^2} + {\left[ {y - \left( { - 5} \right)} \right]^2} + {\left[ {z - \left( { - 1} \right)} \right]^2} = {\left( {\sqrt 2 } \right)^2}\)
Mặt cầu có tâm I(0; -5; -1) và bán kính \(R = \sqrt 2 \).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 3 (SGK Cánh Diều - Tập 2 - Trang 83)
Viết phương trình của mặt cầu, biết:
a) Tâm O bán kính R với O là gốc tọa độ;
b) Đường kính AB với A(1; 2; 1), B(3; 4; 7).
Thảo luận (1)Hướng dẫn giảia) Mặt cầu có tâm O(0; 0; 0) bán kính R có phương trình là: \({x^2} + {y^2} + {z^2} = {R^2}\)
b) Gọi là trung điểm của AB nên I(2; 3; 4). Do đó, mặt cầu đường kính AB có tâm là I(2; 3; 4) và bán kính \(AI = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 - 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {11} \) nên có phương trình là:
\({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 4} \right)^2} = 11\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 4 (SGK Cánh Diều - Tập 2 - Trang 83)
Chứng minh rằng phương trình x2 + y2 + z2 – 6x – 2y – 4z – 11 = 0 là phương trình của một mặt cầu. Tìm tâm I và bán kính R của mặt cầu đó.
Thảo luận (1)Hướng dẫn giảiTa có: \({x^2} + {y^2} + {z^2} - 6x - 2y - 4z - 11 = 0\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 2.x.3 - 2.y.1 - 2.z.2 - 11 = 0\)
\( \Leftrightarrow {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 25\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 5 (SGK Cánh Diều - Tập 2 - Trang 85)
Trong Ví dụ 6, giả sử người đi biển di chuyển theo đường thẳng từ vị trí I(21; 35; 50) đến vị trí D(5 121; 658; 0). Tìm vị trí cuối cùng trên đoạn thẳng ID sao cho người đi biển còn có thể nhìn thấy được ánh sáng từ ngọn hải đăng.
Thảo luận (1)Hướng dẫn giảiĐường thẳng ID đi qua điểm I và nhận \(\overrightarrow {ID} = \left( {5\;100;623; - 50} \right)\) làm một vectơ chỉ phương nên phương trình tham số đường thẳng ID là: \(\left\{ \begin{array}{l}x = 21 + 5\;100t\\y = 35 + 623t\\z = 50 - 50t\end{array} \right.\) (t là tham số).
Gọi H là vị trí cuối cùng trên đoạn ID sao cho người đi biển có thể nhìn thấy ánh sáng từ ngọn hải đăng. Khi đó, \(IH = R\)
Vì H thuộc đường thẳng ID nên \(H\left( {21 + 5\;100t;35 + 623t;50 - 50t} \right)\)
Ta có: \(IH = R \Leftrightarrow \sqrt {{{\left( {5100t} \right)}^2} + {{\left( {623t} \right)}^2} + {{\left( { - 50t} \right)}^2}} = 4000 \Leftrightarrow \sqrt {26\;400\;629{t^2}} = 4000\)
\( \Leftrightarrow t \approx \pm 0,78\)
+ Với \(t \approx 0,78\) ta có H(3 999; 520,94; 11), \(\overrightarrow {IH} = \left( {3\;978;485,94; - 39} \right)\). Khi đó, \(\overrightarrow {ID} = \frac{{50}}{{39}}\overrightarrow {IH} \) nên hai vectơ ID và IH cùng hướng, thỏa mãn H thuộc đoạn thẳng ID.
+ Với \(t \approx - 0,78\) ta có H(-3 999; -450,94; 89), \(\overrightarrow {IH} = \left( { - 3\;978; - 485,94;39} \right)\). Khi đó, \(\overrightarrow {ID} = - \frac{{50}}{{39}}\overrightarrow {IH} \) nên hai vectơ ID và IH ngược hướng, vậy H không thuộc đoạn thẳng ID.
Vậy ví trị cuối cùng trên đoạn thẳng ID sao cho người đi biển còn có thể nhìn thấy được ánh sáng từ ngọn hải đăng là điểm H(3 999; 520,94; 11).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 1 (SGK Cánh Diều - Tập 2 - Trang 85)
Tâm của mặt cầu (S): (x – 2)2 + (y – 3)2 + (z + 4)2 = 16 có tọa độ là:
A. (– 2; – 3; 4). B. (2; 3; – 4). C. (2; – 3; – 4). D. (2; – 3; 4).
Thảo luận (1)Hướng dẫn giảiTa có mặt cầu (S)
\(\left(x-2\right)^2+\left(y-3\right)^2+\left(z+4\right)^2=16\\ \Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2+\left[z-\left(-4\right)\right]^2=16\)
=> Tâm của mặt cầu \(I\left(2;3;-4\right)\)
=> Chọn B
(Trả lời bởi Phong)
Bài tập 2 (SGK Cánh Diều - Tập 2 - Trang 85)
Bán kính của mặt cầu (S): (x – 1)2 + (y – 2)2 + (z – 3)2 = 9 bằng:
A. 3. B. 9. C. 81. D. \(\sqrt{3}\).
Thảo luận (1)Hướng dẫn giải