Bài 2. Tứ giác nội tiếp đường tròn

Hướng dẫn giải

Tứ giác ABCD được gọi là tứ giác nội tiếp đường tròn.

(Trả lời bởi datcoder)

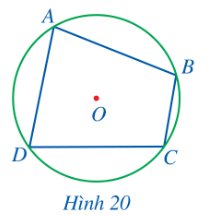
Hướng dẫn giải

Ở Hình 20, các đỉnh A, B, C, D của tứ giác ABCD đều thuộc đường tròn (O).

(Trả lời bởi datcoder)

Hướng dẫn giải

Vẽ đường tròn (O), lấy 4 điểm A, B, C, D (theo thứ tự cùng chiều kim đồng hồ) thuộc đường tròn (O) và nối các đoạn thẳng AB, BC, CD, DA thì ta được tứ giác ABCD có bốn đỉnh thuộc đường tròn (O) (hình vẽ).

(Trả lời bởi datcoder)

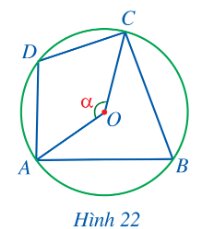
Hướng dẫn giải

a) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)

\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)

b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)

\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)

c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ  -  \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ  -  \alpha +  \alpha}}{2} = 180^\circ .\)

(Trả lời bởi datcoder)

Hướng dẫn giải

Vì tam giác ABC đều nên \(\widehat {ABC} = \widehat {ACB} = 60^\circ .\) Mà tam giác ABC và nội tiếp (O) nên sđ\(\overset\frown{AB}=2\)\(\widehat {ACB}\), sđ\(\overset\frown{AC}=2\)\(\widehat {ABC}\).

Suy ra sđ\(\overset\frown{AB}=\)sđ\(\overset\frown{AC}=2.60{}^\circ =120{}^\circ .\) Do đó

sđ\(\overset\frown{BAC}=\) sđ\(\overset\frown{AB}+\)sđ\(\overset\frown{AC}=120{}^\circ +120{}^\circ =240{}^\circ .\)

Góc BMC là góc nội tiếp chắn cung BAC của (O) nên \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}=\frac{1}{2}.240{}^\circ =120{}^\circ .\)

Vậy \(\widehat {BMC} = 120^\circ .\)

(Trả lời bởi datcoder)

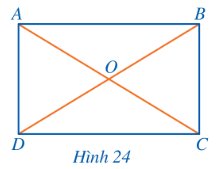
Hướng dẫn giải

Do ABCD là hình chữ nhật nên 2 đường chéo cắt nhau tại trung điểm O của mỗi đường, do đó AO = CO= \(\frac{1}{2}AC\) và OB = OD = \(\frac{1}{2}BD\). Mà AC = BD (tính chất hình chữ nhật)

Suy ra AO = CO = OB = OD = R.

Vậy các điểm A, B, C, D thuộc (O; R).

(Trả lời bởi datcoder)

Hướng dẫn giải

Giả sử ta có hình chữ nhật ABCD nội tiếp đường tròn tâm (O).

Suy ra bán kính đường tròn là OC, đường kính AC.

Hình chữ nhật ABCD có chiều dài AB = 8cm, chiều rộng BC = 6cm. Áp dụng định lý Pytago trong tam giác vuông ABC có:

\(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{8^2} + {6^2}}  = 10cm.\)

Do đó \(R = OC = \frac{{AC}}{2} = \frac{{10}}{2} = 5cm.\)

Diện tích hình tròn là: \(\pi {R^2} = \pi {.5^2} = 25\pi (c{m^2}).\)

Diện tích hình chữ nhật là: \(8.6 = 48(c{m^2}).\)

Diện tích phần tô màu đỏ là: \(25\pi  - 48 \approx 30,5(c{m^2})\) (với \(\pi  \approx 3,14\)).

(Trả lời bởi datcoder)

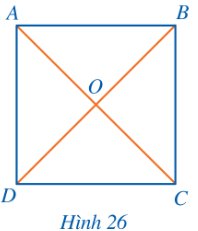
Hướng dẫn giải

a) Vì hình vuông cũng là một hình chữ nhật nên mỗi đường chéo của hình vuông cũng là đường kính của đường tròn ngoại tiếp hình vuông đó.

b) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = 90^\circ \) và OA = OB.

Xét tam giác OAB  vuông tại O, ta có:

 \(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\2O{A^2} = {a^2}\\OA = \frac{{\sqrt 2 a}}{2}.\end{array}\)

Vậy \(OA = \frac{{\sqrt 2 a}}{2}.\)

(Trả lời bởi datcoder)

Hướng dẫn giải

Giả sử hình vuông có cạnh là a, thì bán kính đường tròn ngoại tiếp hình vuông đó là \(\frac{{\sqrt 2 a}}{2}.\)

Chu vi hình vuông là 4a, chu vi của đường tròn ngoại tiếp là \(2\frac{{\sqrt 2 a}}{2}\pi  = \sqrt 2 a\pi .\)

Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: \(\frac{{4a}}{{\sqrt 2 a\pi }} = \frac{{2\sqrt 2 }}{\pi }.\)

(Trả lời bởi datcoder)

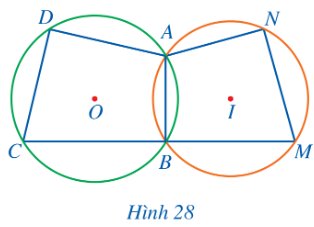
Hướng dẫn giải

Đường tròn (O) là đường tròn ngoại tiếp tứ giác ABCD vì nó đi qua 4 đỉnh A, B, C, D của tứ giác ABCD.

Đường tròn (I) là đường tròn ngoại tiếp tứ giác ABMN vì nó đi qua 4 đỉnh A, B, M, N của tứ giác ABMN.

(Trả lời bởi datcoder)