Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
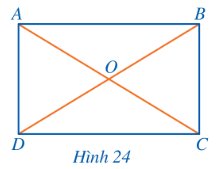
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?

Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.
Thảo luận (1)Hướng dẫn giải
Vì tam giác ABC đều nên \(\widehat {ABC} = \widehat {ACB} = 60^\circ .\) Mà tam giác ABC và nội tiếp (O) nên sđ\(\overset\frown{AB}=2\)\(\widehat {ACB}\), sđ\(\overset\frown{AC}=2\)\(\widehat {ABC}\).
Suy ra sđ\(\overset\frown{AB}=\)sđ\(\overset\frown{AC}=2.60{}^\circ =120{}^\circ .\) Do đó
sđ\(\overset\frown{BAC}=\) sđ\(\overset\frown{AB}+\)sđ\(\overset\frown{AC}=120{}^\circ +120{}^\circ =240{}^\circ .\)
Góc BMC là góc nội tiếp chắn cung BAC của (O) nên \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}=\frac{1}{2}.240{}^\circ =120{}^\circ .\)
Vậy \(\widehat {BMC} = 120^\circ .\)
(Trả lời bởi Nguyễn Quốc Đạt)
Trong Hình 22, cho biết \(\widehat {AOC} = a.\)
Tính số đo của các cung và góc sau theo a.
a) \(\overset\frown{ADC},\widehat{ABC;}\)
b) \(\overset\frown{ADC},\widehat{ABC;}\)
c) \(\widehat{ADC}+\widehat{ABC.}\)
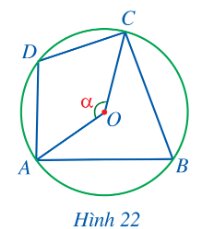
Thảo luận (1)Hướng dẫn giảia) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)
\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)
b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)
\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)
c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ - \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ - \alpha + \alpha}}{2} = 180^\circ .\)
(Trả lời bởi Nguyễn Quốc Đạt)
Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:
- Vẽ một đường tròn
- Vẽ tứ giác có 4 đỉnh thuộc đường tròn.
Thảo luận (1)Hướng dẫn giảiVẽ đường tròn (O), lấy 4 điểm A, B, C, D (theo thứ tự cùng chiều kim đồng hồ) thuộc đường tròn (O) và nối các đoạn thẳng AB, BC, CD, DA thì ta được tứ giác ABCD có bốn đỉnh thuộc đường tròn (O) (hình vẽ).
(Trả lời bởi Nguyễn Quốc Đạt)
Quan sát Hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không?
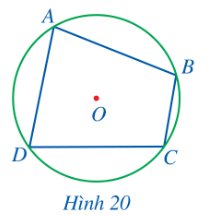
Thảo luận (1)Hướng dẫn giảiỞ Hình 20, các đỉnh A, B, C, D của tứ giác ABCD đều thuộc đường tròn (O).
(Trả lời bởi Nguyễn Quốc Đạt)
Hình 19 minh họa một đường tròn và tứ giác ABCD có bốn đỉnh thuộc đường tròn.
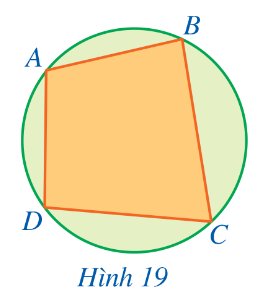
Thảo luận (1)Hướng dẫn giảiTứ giác ABCD được gọi là tứ giác nội tiếp đường tròn.
(Trả lời bởi Nguyễn Quốc Đạt)