Question

Cho hình vuông ABCD, AC cắt BD tại (O) (Hình 26).

a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?

b) Cho biết AB = a, tính OA theo a.

Answer 1

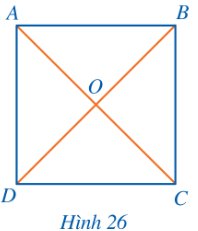
a) Vì hình vuông cũng là một hình chữ nhật nên mỗi đường chéo của hình vuông cũng là đường kính của đường tròn ngoại tiếp hình vuông đó.

b) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = 90^\circ \) và OA = OB.

Xét tam giác OAB  vuông tại O, ta có:

 \(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\2O{A^2} = {a^2}\\OA = \frac{{\sqrt 2 a}}{2}.\end{array}\)

Vậy \(OA = \frac{{\sqrt 2 a}}{2}.\)