Hình chữ nhật \(A\) có chiều rộng \(2x\) (cm), chiều dài gấp \(k\) (\(k > 1\) lần chiều rộng. Hình chữ nhật \(B\) có chiều dài \(3x\) (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì \(B\) phải có chiều rộng bằng bao nhiêu?
Bài 2. Các phép toán với đa thức nhiều biến
Giải mục 3 trang 15,16 (SGK Chân trời sáng tạo)
Thảo luận (1)
Giải mục 3 trang 15,16 (SGK Chân trời sáng tạo)
Thực hiện phép chia \(8{x^4}{y^5}{z^3}\) cho \(2{x^3}{y^4}z\).
Thảo luận (1)Hướng dẫn giải
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.
b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.
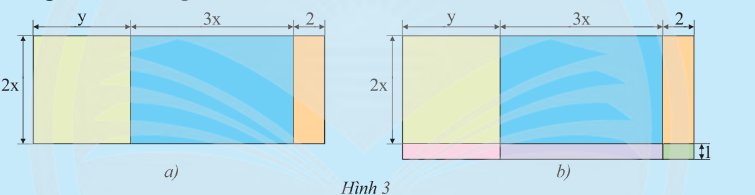
Thảo luận (1)Hướng dẫn giảia) Cách 1: Diện tích sàn là: \(2x.\left( {y + 3x + 2} \right) = 2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
Cách 2: Diện tích sàn là: \(2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
b) Diện tích ban công là: \(1.\left( {y + 3x + 2} \right) = y + 3x + 2\)
Tổng diện tích sàn bao gồm cả ban công là: \(\left( {2xy + 6{x^2} + 4x} \right) + \left( {y + 3x + 2} \right) = 2xy + 6{x^2} + 4x + y + 3x + 2 = 2xy + 6{x^2} + y + 7x + 2\)
(Trả lời bởi Hà Quang Minh)
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
Tính diện tích phần tô màu trong Hình 4.
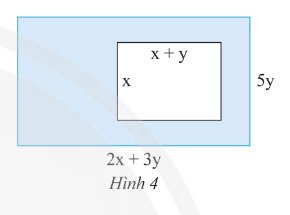
Thảo luận (2)Hướng dẫn giảiDiện tích cả hình: `(2x+3y) . 5y = 10xy + 15y^2`
Diện tích phần không tô màu: `(x+y).x = x^2 + xy`
Diện tích phần tô màu: `10xy + 15y^2 - x^2 - xy = 15y^2 + 9xy -x^2`
(Trả lời bởi Vui lòng để tên hiển thị)
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
Thực hiện các phép nhân:
a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\) b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)
Thảo luận (2)Hướng dẫn giảia) \(\left(-5a^4\right)\cdot\left(a^2b-ab^2\right)\)
\(=\left(-5a^4\cdot a^2b\right)-\left(-5a^4\cdot ab^2\right)\)
\(=-5a^6b+5a^5b^2\)
b) \(\left(x+2y\right)\left(xy^2-2y^3\right)\)
\(=x^2y^2-2xy^3+2xy^3-4y^4\)
\(=x^2y^2-4y^4\)
(Trả lời bởi HT.Phong (9A5))
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
Thực hiện các phép nhân đơn thức sau:
a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right)\) b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right)\) c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2}\)
Thảo luận (2)Hướng dẫn giải`a)`
`4x^3 * (-6x^3y)`
`= 4*(-6) * (x^3*x^3) * y`
`= -24x^6y`
`b)`
`(-2y)*(-5xy^2)`
`= (-2)*(-5)*x*(y*y^2)`
`= 10xy^3`
`c)`
`(-2a)^3 * (2ab)^2`
`= (-8a^3) * (4a^2b^2)`
`= (-8*4)*(a^3*a^2)*b^2`
`= -32a^5b^2`
(Trả lời bởi 『Kuroba ム Tsuki Ryoo...)
Giải mục 1 trang 12 (SGK Chân trời sáng tạo)
Cho hai đa thức \(M = 1 + 3xy - 2{x^2}{y^2}\) và \(N = x - xy + 2{x^2}{y^2}\). Tính \(M + N\) và \(M - N\).
Thảo luận (1)Hướng dẫn giải`M + N = 1 + 3xy - 2x^2y^2 + x - xy + 2x^2y^2`
`= 1 + 2xy + x`.
`M - N = (1+3xy-2x^2y^2)-(x-xy+2x^2y^2)`
`= 1 - x + 4xy - 4x^2y^2`
(Trả lời bởi Vui lòng để tên hiển thị)
Giải mục 1 trang 12 (SGK Chân trời sáng tạo)
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng A, B và C với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá a đồng/{m^2}. Tại đây có hai lần nhập vật liệu như bảng sau:a) Tính tổng số tiền mua kính của cả hai lần.b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Đọc tiếp
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng \(A\), \(B\) và \(C\) với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá \(a\) đồng/\({m^2}\). Tại đây có hai lần nhập vật liệu như bảng sau:
a) Tính tổng số tiền mua kính của cả hai lần.
b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Thảo luận (1)Hướng dẫn giải`a,` Diện tích tấm A: `x^2`
Diện tích tấm B: `x`
Diện tích tấm C: `xy`.
Số tiền mua kính cả 2 lần: `((2x^2 + 4x + 5xy) + (4x^2 + 3x + 6xy)).a(đ)`
`= (6x^2 + 7x + 11xy).a (đ)`.
Số tiền lần 2 hơn lần 1: `-((2x^2 + 4x + 5xy) - (4x^2 + 3x + 6xy))`
`= -(-2x^2 + x - xy).a(đ)`
`= (2x^2 - x + xy).a(đ)`
(Trả lời bởi Vui lòng để tên hiển thị)
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
Hình hộp chữ nhật \(A\) có chiều rộng \(2x\), chiều dài và chiều cao đề gấp \(k\) lần chiều rộng (Hình 2).
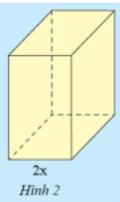
a) Tính diện tích đáy của \(A\).
b) Tính thể tích của \(A\).
Thảo luận (1)Hướng dẫn giảia) Chiều dài, chiều cao hình hộp chữ nhật \(A\) là: \(2xk\)
Diện tích đáy của hình hộp chữ nhật \(A\) là: \(2xk.2x = 4k{x^4}\)
b) Thể tích của hình hộp chữ nhật \(A\) là: \(2xk.2x.2xk = 8{k^2}{x^3}\)
(Trả lời bởi Hà Quang Minh)
Giải mục 2 trang 13,14,15 (SGK Chân trời sáng tạo)
Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ left( {v + 3} right)km/h, ca nô đi ngược dòng với tốc độ left( {2v - 3} right)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian t giờ kể từ khi rời bến?
Đọc tiếp
Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:
Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ \(\left( {v + 3} \right)\)km/h, ca nô đi ngược dòng với tốc độ \(\left( {2v - 3} \right)\)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian \(t\) giờ kể từ khi rời bến?
Thảo luận (1)Hướng dẫn giảiQuãng đường thuyền đi xuôi dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {v + 3} \right)t = vt + 3t\) (km)
Quãng đường ca nô đi ngược dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {2v - 3} \right)t = 2vt - 3t\) (km)
Tổng độ dài quãng đường thuyền và ca nô đi được trong khoảng thời gian \(t\) là:
\(\left( {vt + 3t} \right) + \left( {2vt - 3t} \right) = 3vt\) (km)
Gọi khoảng cách lúc đầu giữa hai phương tiện là \(s\) (km).
Khoảng cách giữa hai phương tiện sau khoảng thời gian \(t\) là:
\(s - 3vt\) (km)
(Trả lời bởi Hà Quang Minh)