Cho mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0 với \(\overrightarrow{n}=\left(A;B;C\right)\) là vectơ pháp tuyến. Cho điểm M0(2; 3; 4). Gọi H(xH; yH; zH) là hình chiếu vuông góc của điểm M0 trên mặt phẳng (P) (Hình 16).
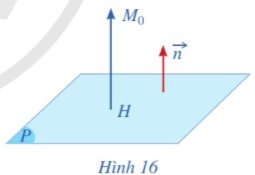
a) Tính tọa độ của \(\overrightarrow{HM_0}\) theo theo xH, yH, zH.
b) Nêu nhận xét về phương của hai vectơ \(\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{HM_0}\).
Từ đó hãy suy ra rằng \(\left|\overrightarrow{n}.\overrightarrow{HM_0}\right|=\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM_0}\right|=\left|A.2+B.3+C.4+D\right|.\)
c) Tính các độ dài \(\left|\overrightarrow{n}\right|,\left|\overrightarrow{HM_0}\right|\) theo A, B, C, D. Từ đó. hãy nêu công thức tính khoảng cách từ điểm M0(2; 3; 4) đến mặt phẳng (P).