Question

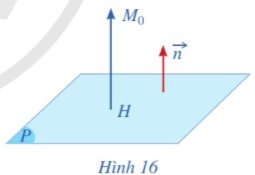
Cho mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0 với \(\overrightarrow{n}=\left(A;B;C\right)\) là vectơ pháp tuyến. Cho điểm M₀(2; 3; 4). Gọi H(x_H; y_H; z_H) là hình chiếu vuông góc của điểm M0 trên mặt phẳng (P) (Hình 16).

a) Tính tọa độ của \(\overrightarrow{HM_0}\) theo theo x_H, y_H, z_H.

b) Nêu nhận xét về phương của hai vectơ \(\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{HM_0}\).

Từ đó hãy suy ra rằng \(\left|\overrightarrow{n}.\overrightarrow{HM_0}\right|=\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM_0}\right|=\left|A.2+B.3+C.4+D\right|.\)

c) Tính các độ dài \(\left|\overrightarrow{n}\right|,\left|\overrightarrow{HM_0}\right|\) theo A, B, C, D. Từ đó. hãy nêu công thức tính khoảng cách từ điểm M₀(2; 3; 4) đến mặt phẳng (P).

Answer 1

a) \(\overrightarrow {H{M_0}} = (2 - {x_H};3 - {y_H};4 - {z_H})\).

b) Vì H là hình chiếu vuông góc của \({M_0}\) trên mặt phẳng (P) nên 2 vecto \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \) cùng phương.

Ta có: \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right|.\left| {\cos \left( {\overrightarrow n ;\overrightarrow {H{M_0}} } \right)} \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right|\).

Lại có: \(\overrightarrow n .\overrightarrow {H{M_0}} = A(2 - {x_H}) + B(3 - {y_H}) + C(4 - {z_H}) \)

\(= A.2 + B.3 + C.4 + ( - A{x_H} - B{y_H} - C{z_H})\)

\(= A.2 + B.3 + C.4 + D\).

\( \Rightarrow \left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\).

Vậy \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\).

c) \(\left| {\overrightarrow n } \right| = \sqrt {{A^2} + {B^2} + {C^2}} \)

\(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right|}}{{\left| {\overrightarrow n } \right|}} = \frac{{\left| {A.2 + B.3 + C.4 + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Vậy công thức tính khoảng cách từ điểm \({M_0}(2;3;4)\) đến mặt phẳng (P) là \(d({M_0};(P)) = \frac{{\left| {A.2 + B.3 + C.4 + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).