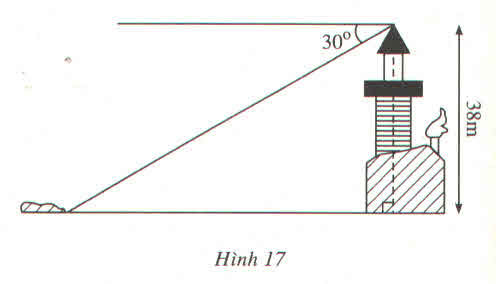
Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc \(30^0\) so với đường nằm ngang chân đèn (h.17). Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu ?
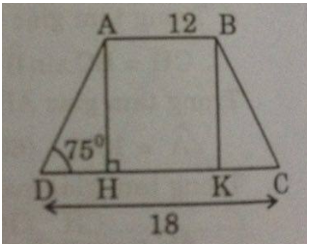
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)