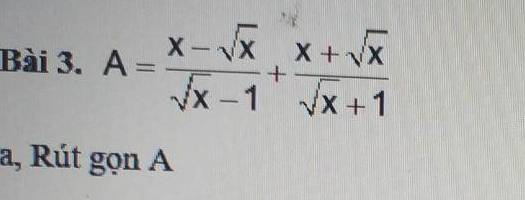a, Ta có:
\(\Delta'=\left[-\left(m-5\right)\right]^2-\left(-4m+1\right)\\ =m^2-10m+25+4m-1\\ =m^2-6m+24\\ =\left(m^2-6m+9\right)+15\\ =\left(m-3\right)^2+15>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m-10\\x_1x_2=-4m+1\end{matrix}\right.\)
\(2x^2_1+2x^2_2+x^2_1x_2+x_1x^2_2=6\\ \Leftrightarrow2\left(x_1+x_2\right)^2-4x_1x_2+x_1x_2\left(x_1+x_2\right)=6\\ \Leftrightarrow2\left(2m-10\right)^2-4\left(-4m+1\right)+\left(-4m+1\right)\left(2m-10\right)=6\\ \Leftrightarrow....\\ \Leftrightarrow m=\dfrac{90}{11}\)
a: \(\text{Δ}=\left(2m-10\right)^2-4\left(-4m+1\right)\)
\(=4m^2-40m+100+16m-4\)
\(=4m^2-24m+96\)
\(=4\left(m^2-6m+24\right)\)
\(=4\left(m-3\right)^2+60>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
b: Theo đề, ta có: \(2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+x_1x_2\left(x_1+x_2\right)=6\)
\(\Leftrightarrow2\cdot\left[\left(2m-10\right)^2-2\left(-4m+1\right)\right]+\left(-4m+1\right)\left(2m-10\right)=6\)
\(\Leftrightarrow2\left(4m^2-40m+100+8m-2\right)-8m^2+40m+2m-20=6\)
\(\Leftrightarrow2\left(4m^2-32m+98\right)-8m^2+42m-20=6\)
\(\Leftrightarrow8m^2-64m+196-8m^2+42m-20=6\)
=>-22m+176=6
=>-22m=-170
hay m=85/11