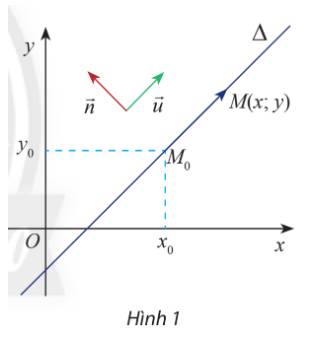
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
a) Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {5; - 3} \right)\), nên ta có phương trình tham số của \(\Delta \) là :
\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 1 - 3t\end{array} \right.\)
Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 1) + 5(y - 1) = 0 \Leftrightarrow 3x + 5y - 8 = 0\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = 2t\\y = - 7t\end{array} \right.\)
Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {7;2} \right)\) và đi qua \(O(0;0)\)
Ta có phương trình tổng quát là
\(7(x - 0) + 2(y - 0) = 0 \Leftrightarrow 7x + 2y = 0\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {MN} = ( - 4;3)\) và có vectơ pháp tuyến \(\overrightarrow n = (3;4)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 4 - 4t\\y = 3t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(3(x - 4) + 4(x - 0) = 0 \Leftrightarrow 3x + 4y - 12 = 0\)