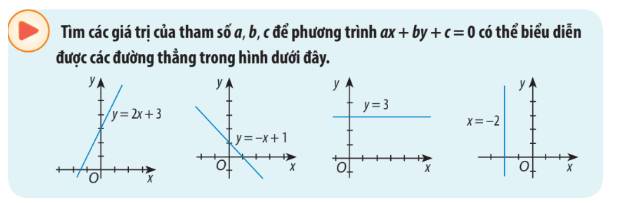
Bài 2: Đường thẳng trong mặt phẳng tọa độ
Khởi động (SGK Chân trời sáng tạo trang 46-51)
Thảo luận (1)
Khám phá 1 (SGK Chân trời sáng tạo trang 46-51)
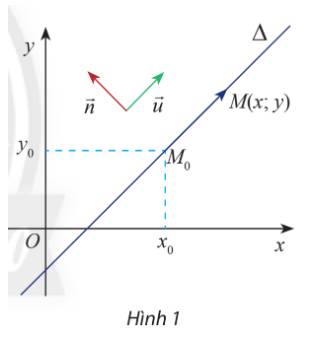
Trong mặt phẳng Oxy, cho hai đường thẳng Delta đi qua điểm {M_0}left( {{x_0};{y_0}} right) và vectơ overrightarrow n left( {a;b} right) và overrightarrow u left( {b; - a} right) khác vectơ 0. Cho biết overrightarrow u có giá song song hoặc trùng với Delta .a) Tính tích vô hướng overrightarrow n overrightarrow {.u} và nêu nhận xét về phương của hai vectơ overrightarrow n ,overrightarrow u b) Gọi Mleft( {x;y} right) là điểm di động trên Delta . Chứng tỏ rằng vectơ overrightarrow {{M_0}M} l...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
Thảo luận (1)Hướng dẫn giảia) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
(Trả lời bởi Hà Quang Minh)
Khám phá 2 (SGK Chân trời sáng tạo trang 46-51)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {{u_1};{u_2}} \right)\) là vectơ chỉ phương. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), tìm tọa độ của điểm M theo tọa độ của \({M_0}\) và \(\overrightarrow u \)
Thảo luận (1)Hướng dẫn giải\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\) mà \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương nên ta có:
\(\left\{ \begin{array}{l}{x_0} - x = {u_1}\\{y_0} - y = {u_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - {u_1}\\y = {y_0} - {u_2}\end{array} \right.\)
Vậy \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
(Trả lời bởi Hà Quang Minh)
Thực hành 1 (SGK Chân trời sáng tạo trang 46-51)
a) Viết phương trình tham số của đường thẳng d đi qua điểm \(B( - 9;5)\) và nhận \(\overrightarrow v = (8; - 4)\) là vectơ chỉ phương
b) Tìm tọa độ điểm P trên \(\Delta \),biết P có tung độ bằng 1.
Thảo luận (1)Hướng dẫn giảia) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = - 9 + 8t\\y = 5 - 4t\end{array} \right.\)
b) Thay \(y = 1\) vào phương trình \(y = 5 - 4t\) ta được \(1 = 5 - 4t \Rightarrow t = 1\)
Thay \(t = 1\) vào phương trình \(x = - 9 + 8t\), ta được \(x = - 1\)
Vậy \(P( - 1;1)\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Chân trời sáng tạo trang 46-51)
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm M(1;1) với Vectơ vận tốcoverrightarrow v (40;30)a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tôb) Tìm tọa độ của xe tương ứng với t 2; t 4
Đọc tiếp
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v = (40;30)\)
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4

Thảo luận (1)Hướng dẫn giảia) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)
(Trả lời bởi Hà Quang Minh)
Khám phá 3 (SGK Chân trời sáng tạo trang 46-51)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
Thảo luận (1)Hướng dẫn giải\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho
(Trả lời bởi Hà Quang Minh)
Thực hành 2 (SGK Chân trời sáng tạo trang 46-51)
Viết phương trình tham số và phương trình tổng quát của đường thẳng Delta trong các trường hợp sau:a) Đường thẳng Delta đi qua điểm A(1;1)và có vectơ pháp tuyến overrightarrow n left( {3;5} right)b) Đường thẳng Delta đi qua gốc tọa độ O(0;0)và có vectơ chỉ phương overrightarrow u left( {2; - 7} right)c) Đường thẳng Delta đi qua hai điểm M(4;0),N(0;3)
Đọc tiếp
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {5; - 3} \right)\), nên ta có phương trình tham số của \(\Delta \) là :
\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 1 - 3t\end{array} \right.\)
Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 1) + 5(y - 1) = 0 \Leftrightarrow 3x + 5y - 8 = 0\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = 2t\\y = - 7t\end{array} \right.\)
Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {7;2} \right)\) và đi qua \(O(0;0)\)
Ta có phương trình tổng quát là
\(7(x - 0) + 2(y - 0) = 0 \Leftrightarrow 7x + 2y = 0\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {MN} = ( - 4;3)\) và có vectơ pháp tuyến \(\overrightarrow n = (3;4)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 4 - 4t\\y = 3t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(3(x - 4) + 4(x - 0) = 0 \Leftrightarrow 3x + 4y - 12 = 0\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Chân trời sáng tạo trang 46-51)
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm M(x;y) từ vị trí A(1;2) chuyển động thẳng đều với Vectơ vận tốc overrightarrow v (3; - 4)a) Viết phương trình tổng quát của đường thẳng Delta biểu diễn đường đi của điểm Mb) Tìm tọa độ của điểm M khi Delta cắt trục hoành
Đọc tiếp
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm \(M(x;y)\) từ vị trí \(A(1;2)\) chuyển động thẳng đều với Vectơ vận tốc \(\overrightarrow v = (3; - 4)\)
a) Viết phương trình tổng quát của đường thẳng \(\Delta \) biểu diễn đường đi của điểm M
b) Tìm tọa độ của điểm M khi \(\Delta \) cắt trục hoành
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow v = \left( {3; - 4} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {4;3} \right)\) và đi qua \(A(1;2)\)
Ta có phương trình tổng quát là
\(4(x - 1) + 3(y - 2) = 0 \Leftrightarrow 4x + 3y - 10 = 0\)
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay \(y = 0\) vào phương trình \(4x + 3y - 10 = 0\) ta tìm được \(x = \frac{5}{2}\)
Vậy \(\Delta \) cắt trục hoành tại điểm \(M\left( {\frac{5}{2};0} \right)\)
(Trả lời bởi Hà Quang Minh)
Thực hành 3 (SGK Chân trời sáng tạo trang 46-51)
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2.
Thảo luận (1)Hướng dẫn giảia) Ta có \(3x + 5y - 8 = 0 \Leftrightarrow y = \frac{8}{5} - \frac{3}{5}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 5y - 8 = 0\) là \(y = \frac{8}{5} - \frac{3}{5}x\)
b) Ta có \(7x + 2y = 0 \Leftrightarrow y = - \frac{7}{2}x\)
Vậy hàm số bậc ứng với đường thẳng \(7x + 2y = 0\) là \(y = - \frac{7}{2}x\)
c) Ta có \(3x + 4y - 12 = 0 \Leftrightarrow y = 3 - \frac{3}{4}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 4y - 12 = 0\) là \(y = 3 - \frac{3}{4}x\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 3 (SGK Chân trời sáng tạo trang 46-51)
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 {m^3}/h vào một cái bể đã chứa sẵn 5 {m^3} nước.a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờb) Gọi y f(x)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số nàyc) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Đọc tiếp
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 \({m^3}/h\) vào một cái bể đã chứa sẵn 5 \({m^3}\) nước.
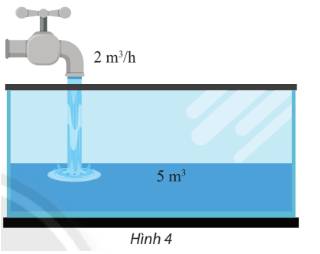
a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ
b) Gọi \(y = f(x)\)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Thảo luận (1)Hướng dẫn giảia) Thể tích nước trong bể được tính bằng công thức \(y = 5 + 2x\)
b)
c) Ta có đồ thị hàm số bậc nhất \(y = 5 + 2x \Leftrightarrow 2x - y + 5 = 0\)
Vậy phương trình tổng quát của đường thẳng d là \(2x - y + 5 = 0\)
Từ phương trình tổng quát ta có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1} \right)\), từ đó ta có vectơ chỉ phương \(\overrightarrow u = (1;2)\)
Khi \(x = 0\) thì \(y = 5\) nên đường thẳng đó đi qua điểm \((0;5)\)
Ta có phương trình tham số của đường thẳng d là \(\left\{ \begin{array}{l}x = t\\y = 5 + 2t\end{array} \right.\)
(Trả lời bởi Hà Quang Minh)
