Question

Vẽ hình thì càng tốt nha (cấm sử dụng kiến thức chưa học), vi phạm = báo cáo

Cho \(\Delta\)\(ABC\) cân tại A. Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB. Gọi I là giao điểm của MN và BC. CMR: I là trung điểm của MN

Answer 1

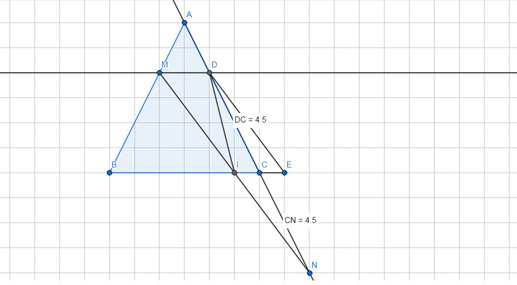
- Kẻ MD//BC (D thuộc AC). Trên tia đối của tia CI lấy điểm E sao cho CI=CE.

- Ta có: Góc ABC=Góc AMD (MD//BC và đồng vị).

Góc ACB=Góc ADM (MD//BC và đồng vị).

Góc ABC=Góc ACB (Tam giác ABC cân tại A).

=>Góc AMD=Góc ADM.

=> Tam giác ADM cân tại A.

=> AD=AM.

*AM+AN=2AB =>AD+AN=2AB  =>AD+AN=2AC

Mà AD+DC=AC nên DC+AC=AN=AC+CN =>DC=CN hay C là trung điểm DN.

- Xét tam giác ICN và tam giác ECD có:

IC=CE (gt)

Góc ICN= Góc ECD (đối đỉnh)

DC=CN (cmt)

=> Tam giác ICN= Tam giác ECD (c-g-c).

=> IN=DE (2 cạnh tương ứng).

Góc INC= Góc EDC (2 góc tương ứng) mà 2 góc này ở vị tri so le trong nên DE//IN.

- Xét tam giác MDI và tam giác EID có:

Góc MDI=Góc EID (MD//IE và so le trong).

DI là cạnh chung.

Góc MID= Góc EDI (MI//DE và so le trong).

=> Tam giác MDI= Tam giác EID (g-c-g)

=>MI=DE (2 cạnh tương ứng ) mà IN=DE (cmt) nên MI=IN hay I là trung điểm MN.

 

 

 

Answer 2