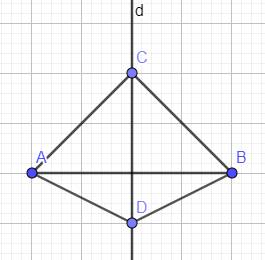
Có `C in d` và `d` là trung trực của `AB=>AC=BC`
`D in d` và `d` là trung trực của `AB=>AD=BD`
Xét `Delta ACD` và `Delta BCD` có :
`{:(AC=BC(cmt)),(CD-chung),(AD=BD(cmt)):}}`
`=>Delta ACD=Delta BCD(c.c.c)(đpcm)`
Cho tam giác ABC cân tại A có d là đường trung trực AB vẽ phân giác AE của góc BAC ( E thuộc BC ) d cắt AE tại O a, AE là đường trung trực của tam giác ABC b, O thuộc đường trung trực của đoạn thẳng AC c, O cách đều 3 đỉnh của tam giác ABC
Cho góc xOy khác góc bẹt Oz là tia phân giác của góc xOy. Gọi M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:
a)Điểm O thuộc đường trung trực của AB
b)OM là đường trung trực của AB
c)Điểm M thuộc đường trung trực của CD
Cho đoạn thẳng AB=5cm. Vẽ đường tròn tâm A bán kính 4cm và đường tròn tâm B bán kính 3cm. Hai đường tròn này cắt nhau tại D,E. Chứng minh:
a)Điểm A thuộc đường trung trực của DE
b)AB là đường trung trực của DE
c)góc ADB=90 độ
Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm
a) Tính độ dài canh AC và so sánh các góc của tam giác ABC.
b) Trên tia đối của tia AB lấy điểm D sao cho AD=AB. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt canh AC tại M. Chứng minh BC=CD và tính độ dài đoạn thẳng AM.
c) Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q. Chứng minh ba điểm B, M, Q thẳng hàng.
Jup mk vs mk cám ơn!
cho đoạn thẳng AB = 5 cm vẽ đường tròn tâm A bán kính 4 cm và đường tròn tâm B bán kính 3 cm hai đường tròn này căt nhau tai D,E .chứng minh :
a)diểm A thuộc đường trung trực của DE
b) AB là đuongf trung trực của DE
c) góc ADB = 90 độ
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ DEBC (EBC).Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh:
1. ABD =EBD
2. BD là đường trung trực của đoạn thẳng AE
3. AD < DC
4. và E, D, F thẳng hàng.
Cho góc ABC cân tại A. Vẽ AH vuông BC (H thuộc BC).
a)Gọi M là trung điểm AB. Đường thẳng vuông góc với AB tại M cắt AH tại E. Chứng minh tam giác AEB cân.
b) Trên cạnh AB, AC lần lượt lấy các điểm D, F sao cho BD = AF. Chứng minh EF > DF/2
Giup mình với :(
cho ∆ abc. trên cạnh bc lấy điểm m sao cho bm = 2cm. vẽ điểm d sao cho c là trung điểm của ad. gọi n là trung điểm của bd. chứng minh : a, m là trọng tâm của ∆ abd. b, ba điểm a, m, n, thẳng hàng. c, đường thẳng dm đi qua trung điểm của ab
Cho đoạn thẳng AB có trung điểm M. Tập hợp các điểm C sao cho tam giác ABC là tam giác cân có đáy là AB là:
đường trung trực của AB.
một đường thẳng đi qua trung điểm M của AB, không lấy điểm M.
một đường thẳng đi qua trung điểm M của AB.
đường trung trực của AB, không lấy trung điểm M của AB.
