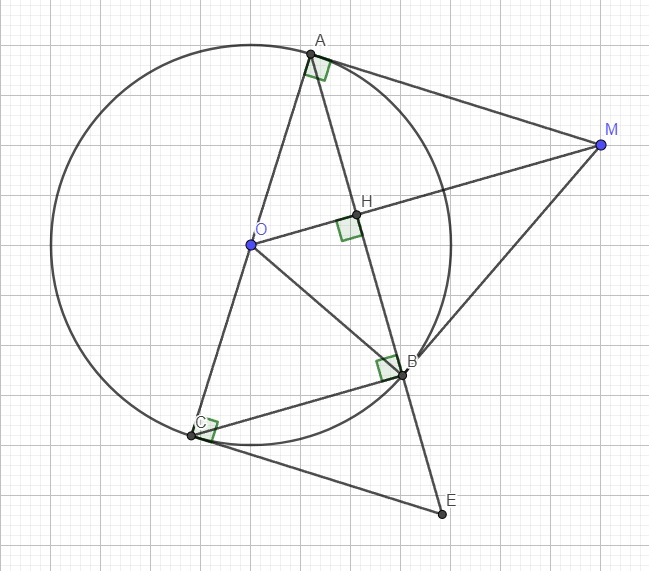
Từ điểm M nằm ngoài (O), kẻ tiếp tuyến MA với (O), (A là tiếp điểm). Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B ( B khác A). Kẻ đường kính AC của (O). Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E. a) CM: 4 điểm E,H,O,C cùng thuộc 1 đường tròn b) CM: Tam giác AMB cân c) CM: BE.BM=BC.BO
a. Em tự giải
b.
\(\Delta OAB\) cân tại O (do \(OA=OB=R\), mà \(OH\) là đường vuông góc (do OH vuông góc AB)
\(\Rightarrow OH\) đồng thời là trung tuyến và trung trực của AB
Hay OM là trung trực của AB
\(\Rightarrow MA=MB\Rightarrow\Delta MAB\) cân tại M
c.
Do EC là tiếp tuyến tại C \(\Rightarrow EC\perp AC\)
MA là tiếp tuyến tại A \(\Rightarrow MA\perp AC\)
\(\Rightarrow EC||MA\Rightarrow\widehat{MAH}=\widehat{CEB}\) (so le trong)
Mà \(\widehat{MAH}=\widehat{MOA}\) (cùng phụ \(\widehat{AMH}\))
\(\Rightarrow\widehat{CEB}=\widehat{MOA}\)
Xét hai tam giác CEB và MOA có:
\(\left\{{}\begin{matrix}\widehat{CEB}=\widehat{MOA}\left(cmt\right)\\\widehat{CBE}=\widehat{MAO}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta CEB\sim\Delta MOA\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{OA}=\dfrac{BC}{AM}\Rightarrow BE.AM=BC.OA\)
Mà \(MA=MB\) (theo cm câu b) và \(OA=BO=R\)
\(\Rightarrow BE.BM=BC.BO\)
a: Xét tứ giác EHOC có \(\widehat{EHO}+\widehat{ECO}=90^0+90^0=180^0\)
nên EHOC là tứ giác nội tiếp
=>E,H,O,C cùng thuộc một đường tròn
b: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOB
Xét ΔAOM và ΔBOM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔAOM=ΔBOM
=>MA=MB
=>ΔMAB cân tại M
c: Ta có: ΔAOM=ΔBOM
=>\(\widehat{OAM}=\widehat{OBM}=90^0\)
Xét tứ giác OAMB có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>\(\widehat{OMB}=\widehat{OAB}=\widehat{CAB}\left(1\right)\)
Xét (O) có
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
\(\widehat{ECB}\) là góc tạo bởi tiếp tuyến CE và dây cung CB
Do đó: \(\widehat{CAB}=\widehat{ECB}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{OMB}=\widehat{ECB}\)
Xét ΔOMB và ΔECB có
\(\widehat{OMB}=\widehat{ECB}\)
\(\widehat{OBM}=\widehat{EBC}=90^0\)
Do đó: ΔOMB~ΔECB
=>\(\dfrac{BO}{BE}=\dfrac{BM}{BC}\)
=>\(BO\cdot BC=BM\cdot BE\)
a.
Do \(OH\perp AB\Rightarrow\Delta OHE\) vuông tại H
\(\Rightarrow\) Tam giác OHE nội tiếp đường tròn đường kính OE (1)
Do CE là tiếp tuyến tại C \(\Rightarrow CE\perp OC\)
\(\Rightarrow\Delta OCE\) vuông tại C
\(\Rightarrow\) Tam giác OCE nội tiếp đường tròn đường kính OE (2)
(1);(2) \(\Rightarrow4\) điểm E,H,O,C cùng thuộc đường tròn đường kính OE