Ôn thi vào 10
Các câu hỏi tương tự
Cho đường tròn (O) bán kính R. Từ điểm A nằm bên ngoài đường tròn vẽ hai tiếp tuyến AC, AB (B, C là các tiếp điểm). Kẻ cát tuyến AMN tới đường tròn, gọi D là trung điểm của dây MNa) Chứng minh rằng 5 điểm A, O, B, C, D cùng nằm trên một đường trònb) Cho ACOC. Hãy chứng minh tứ giác ACOB là hình vuông và tính diện tích đường tròn ngoại tiếp tứ giác ACOB theo R.c) Kẻ ME ⊥ AB (E ∈ AB), MF ⊥ AC (F ∈ AC), MK ⊥ BC (K ∈ BC). Chứng minh góc KME bằng góc KMFd) Gọi H là giao điểm của MB và KE, I là giao đ...
Đọc tiếp
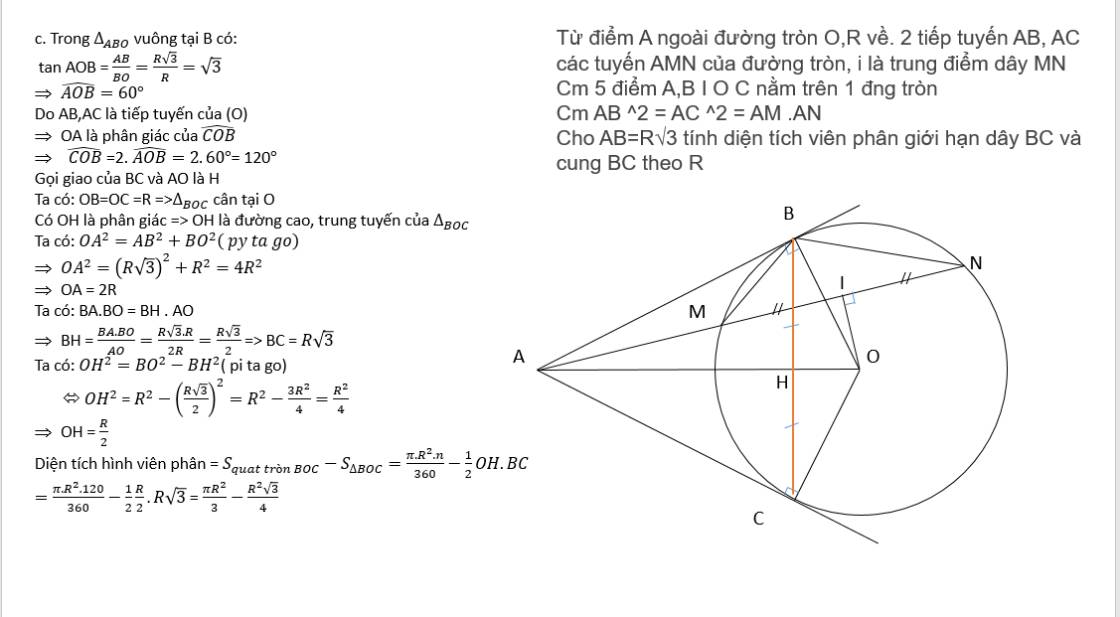
Cho đường tròn (O) bán kính R. Từ điểm A nằm bên ngoài đường tròn vẽ hai tiếp tuyến AC, AB (B, C là các tiếp điểm). Kẻ cát tuyến AMN tới đường tròn, gọi D là trung điểm của dây MN
a) Chứng minh rằng 5 điểm A, O, B, C, D cùng nằm trên một đường tròn
b) Cho AC=OC. Hãy chứng minh tứ giác ACOB là hình vuông và tính diện tích đường tròn ngoại tiếp tứ giác ACOB theo R.
c) Kẻ ME ⊥ AB (E ∈ AB), MF ⊥ AC (F ∈ AC), MK ⊥ BC (K ∈ BC). Chứng minh góc KME bằng góc KMF
d) Gọi H là giao điểm của MB và KE, I là giao điểm của MC và KF. Chứng minh MK² = ME . MF
e) Chứng minh tứ giác MHKI nội tiếp và HI // BC.
Ai đó có thể giúp mình phần d và e không, chứ mình thì chịu với nó rồi. Ngày mai mình phải nộp rồi, các bạn giúp mình với.
từ điểm A ở ngoài đường tròn O , vẽ 2 tiép tuyến AB,AC và 2 cát tuyến AMN với đường tròn ( B,C là các tuyến điểm , AM<AN và tia AM nằm giữa 2 tí AB,AO) gọi I là hình chiếu của O trên AN , H là giao điểm của OA và BC .chứng minh
A/ IA là tia phân giác góc BIC
thank :333
Từ một điểm A nằm ngoài đường tròn tâm O bán kính R,kẻ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm).Trên cung nhỏ Bc lấy một điểm M bất kì khác B và C.Gọi I , K , P lần lượt là hình chiếu vuông góc của điểm M trên các đoạn thẳng AB,AC,BC.
Chứng minh AIMK là tứ giác nội tiếp.
Từ điểm A cố định nằm ngoài đường tròn (O;R), dựng các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn (B,C thuộc (O), D nằm giữa A và E). Gọi I là trung điểm của DE, H là giao điểm của AO và BC.
Qua I kẻ đường thẳng song song với BE, cắt BC tại M. Chứng minh rằng DM vuông góc với BO
B11:Từ 1 điểm A nằm ngoài đường tròn (O;R)ta vẽ hai tiếp tuyến AB,AC với đường tròn (B,C là tiếp điểm).Trên cung nhỏ BC lấy 1 điểm M,vẽ\(MI\perp AB,MK\perp AC\left(I\in AB,K\in AC\right)\)
a)Chứng minh:AIMK là tứ giác nội tiếp đường tròn.
b)Vẽ MP\(\perp\)BC(P\(\perp\)BC).Chứng minh: Góc MPK = Góc MBC
Cho đường tròn (O,R) dây cung MN (MN<2R) .Trên tia dối của tia MN lấy điểm A. từ A kẻ tiếp tuyến AAB<AC tới đường tròn O.
c) GỌi I là trung điểm của MN. Kẻ BI cắt dường tròn tại E. Cm EC//với AN.
(gợi ý:Nên Cm tứ giác OBAC nội tiếp và Cm AB2 =AC2 =AM.AN để cm câu c)
từ điểm A ở ngoài đường tròn O , vẽ 2 tiếp tuyến AB , AC và cát tuyến AMN với đường tròn ( B,C là tiếp tuyến AM<AN và tia AM nắm giữa 2 tai AB,AO) gọi I là hình chiếu của O trên AN , H là giao điểm của OA và BC
a/ IA là tia phân giác của góc BIC
B/ điểm H thuộc đường tròn ngoại tiếp tam giác OMN
thank
Câu 3 Cho đường tròn (O; R). Từ một điểm C bên ngoài đường tròn (O), kẻ hai tiếp tuyến CM, CN và cát tuyến CAB với đường tròn (A nằm giữa C và B). Gọi H là trung điểm của dây AB, đường thẳng HO cắt đường thẳng CN tại K, đường thẳng MH cắt đường tròn tâm O tại điểm thứ hai là J.1. Chứng minh bốn điểm C, H, O, N cùng nằm trên một đường tròn.2. Chứng minh KN. KC KH. KO và NJ //AB.
Đọc tiếp
Câu 3 Cho đường tròn (O; R). Từ một điểm C bên ngoài đường tròn (O), kẻ hai tiếp tuyến CM, CN và cát tuyến CAB với đường tròn (A nằm giữa C và B). Gọi H là trung điểm của dây AB, đường thẳng HO cắt đường thẳng CN tại K, đường thẳng MH cắt đường tròn tâm O tại điểm thứ hai là J.
1. Chứng minh bốn điểm C, H, O, N cùng nằm trên một đường tròn.
2. Chứng minh KN. KC = KH. KO và NJ //AB.
cho đường tròn (O) ,từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC (B,C là hai tiếp điểm).Gọi M là giao điểm OA và BC,D là một điểm nằm trên đường tròn (O) sao cho D không nằm trên đường thẳng OA,kẻ dây cung DE đi qua M.CMR:Tứ giác ADOE nội tiếp.