Question

Trong mặt phẳng với hệ tọa độ Oxy , cho \(\Delta ABC\) nội tiếp đường tròn tâm I(1,0) .Đường thẳng vuông góc với AI tại I cắt AB,AC tại M ,N  sao cho BM.CN=50 .Viết pt AC biết P(3,11) thuộc đường thẳng AB ,M thuộc đương thẳng x+y+7=0 và M có hoành độ âm

Answer 1

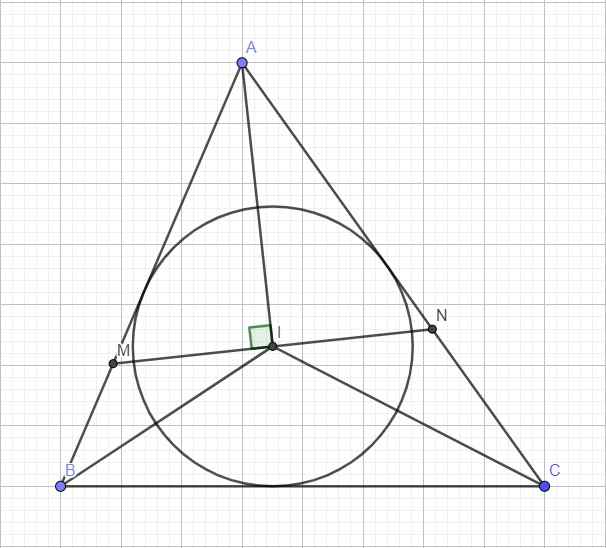
ABC nội tiếp (I) hay (I) là đường tròn nội tiếp tam giác ABC vậy nhỉ?

Answer 2

I là tâm đường tròn nội tiếp nên nó là giao 3 đường phân giác

MN vuông góc AI \(\Rightarrow\) tam giác AMN cân tại A \(\Rightarrow IM=IN\)

Ta có: \(\widehat{AMI}=90^0-\widehat{MAI}=90^0-\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}\left(180^0-\widehat{A}\right)=\dfrac{1}{2}\left(\widehat{B}+\widehat{C}\right)\)

Mà \(\widehat{AMI}=\widehat{MBI}+\widehat{BIM}=\dfrac{1}{2}\widehat{B}+\widehat{BIM}\)

\(\Rightarrow\dfrac{1}{2}\left(\widehat{B}+\widehat{C}\right)=\dfrac{1}{2}\widehat{B}+\widehat{BIM}\Rightarrow\widehat{BIM}=\dfrac{1}{2}\widehat{C}=\widehat{NCI}\)

Hoàn toàn tương tự, ta có \(\widehat{CIN}=\widehat{MBI}\)

\(\Rightarrow\Delta MBI\sim\Delta NIC\Rightarrow\dfrac{BM}{IN}=\dfrac{IM}{NC}\Rightarrow BM.CN=IN.IM=IM^2\)

\(\Rightarrow IM^2=50\)

\(\Rightarrow\) M thuộc đường tròn tâm I có phương trình: \(\left(x-1\right)^2+y^2=50\)

Kết hợp M thuộc \(x+y+7=0\) và \(x_M< 0\Rightarrow M\left(-6;-1\right)\)

Tới đây coi như xong rồi

Tính \(\overrightarrow{MP}\Rightarrow\) phương trình AB

Tính \(\overrightarrow{MI}\Rightarrow\) phương trình AI (qua I và vuông góc IM)

\(\Rightarrow\) Tọa độ A

Tính tọa độ N (I là trung điểm MN)

\(\Rightarrow\overrightarrow{AN}\Rightarrow\) phương trình AC

Answer 3