Ta có: \(\widehat{AKI}=\widehat{ABC}\)
\(\Rightarrow\) IK // BC
Mà K là trung điểm của AB
\(\Rightarrow IK\) là đường trung bình của tam giác ABC
\(\Rightarrow\) I là trung điểm của AC
\(\Rightarrow AI=IC=10cm\)
Vậy x= 10cm
Ta có: \(\widehat{AKI}=\widehat{ABC}\)
\(\Rightarrow\) IK // BC
Mà K là trung điểm của AB
\(\Rightarrow IK\) là đường trung bình của tam giác ABC
\(\Rightarrow\) I là trung điểm của AC
\(\Rightarrow AI=IC=10cm\)
Vậy x= 10cm
Cho tam giác BAC vuông tại A và B'A'C' đồng dạng với BAC có AB=6 BC=10 có BD cắt AC đoạn từ A đến D cho là x và từ Đó đến C cho là y biết y lớn hơn x
a) tính điện tích ABC
b) tính tỉ số x/y
c) tính độ dài x,y
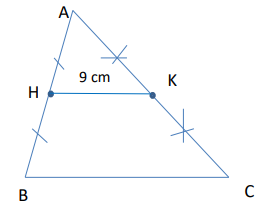
Tính đoạn BC trong hình vẽ.
Cho \(P=\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\)
và \(Q=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
Chứng minh nếu P=1 thì Q=0
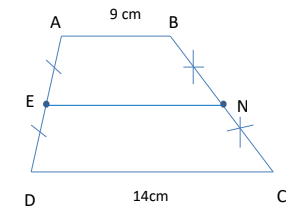
Câu 9. Cho hình thang ABCD ( đáy AB// CD) . Tính EN
Tính giá trị của biểu thức
A= \(\dfrac{x^5-5x^3-4x+2}{x^4+x^2-14x-4}\) biết x2 - 2x - 1 = 0
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Gọi AM là trung tuyết của tam giác ABC. Kẻ MD vuông góc AB, kẻ ME vuông góc AC.
a) Chứng minh tam giác ABC vuông.
b) Tính độ dài AM
c) Tính độ dài DE
d) Chứng minh tứ giác BDEC là hình thang
e) Chứng minh tứ giác BDEM là hình bình hành
f) Chứng minh tứ giác ADME là hình chữ nhật
g) Khi AB = AC tứ giác ADME là hình gì ?
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Gọi AM là trung tuyết của tam giác ABC. Kẻ MD vuông góc AB, kẻ ME vuông góc AC. a) Chứng minh tam giác ABC vuông. b) Tính độ dài AM c) Tính độ dài DE d) Chứng minh tứ giác BDEC là hình thang e) Chứng minh tứ giác BDEM là hình bình hành f) Chứng minh tứ giác ADME là hình chữ nhật g) Khi AB = AC tứ giác ADME là hình gì ?
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Gọi M,N lần lượt là trung điểm của AO và BO.
1/ Cho AB = 8cm ; BC = 10cm.
a/ Tính diện tính hình chữ nhật ABCD.
b/ C/m DMNC là hình thang cân.
2/ Giả sử AC = 2AD. Gọi E là giao điểm của tia CN và tia DM. C/m tứ giác ADOE là hình thoi.
Bài 3: Cho tam giác ABC cân tại A, Gọi D; E thứ tự là trung điểm của AB; AC.
a. Chứng minh rằng BCED là hình thang cân
b. Biết BC = 24 cm. Tính độ dài đường trung bình của hình thang BCED
c. Gọi F là trung điểm của BE; K là trung điểm của DC. Tính FK
1.Tìm giá trị nhỏ nhất của P=\(\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
Q=\(\dfrac{3x^2+2x+3}{x^2+1}\)
RÁNG GIẢI GIÚP MÌNH NHA! CẢM ƠN CÁC BẠN TRƯỚC!