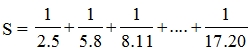\(S=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{17.20}\)
\(S=3.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{17}-\frac{1}{20}\right)\)
\(S=3.\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(S=3.\frac{9}{20}=\frac{27}{20}\)
\(\Rightarrow3S=\frac{3}{2.5}+\frac{3}{3.8}+\frac{3}{8.11}+...+\frac{3}{17.20}\)
\(\Rightarrow3S=\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{17}-\frac{1}{20}\)
\(\Rightarrow3S=\frac{1}{2}-\frac{1}{20}=\frac{9}{20}\Rightarrow S=\frac{3}{20}\)
S = 1/2.5 + 1/5.8 + 1/8.11 + ... + 1/17.20
S = 3/3(1/2.5 + 1/5.8 + 1/8.11 +...+ 1/17.20)
S = 1/3(3/2.5 + 3/5.8 + 3/8.11 +...+3/17.20)
S = 1/3(1/2-1/5+1/5-1/8+1/8-1/11+...+1/17-1/20)
S = 1/3(1/2-1/20)
S = 1/3.9/20
S = 3/20
\(\dfrac{1}{2.5}\)+\(\dfrac{1}{5.8}+\dfrac{1}{8.11}+......+\dfrac{1}{17.20}\)
=\(\dfrac{1}{3}.\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+\dfrac{3}{8.11}+.....+\dfrac{3}{17.20}\right)\)
=\(\dfrac{1}{3}.\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+....+\dfrac{1}{17}-\dfrac{1}{20}\right)\)
=\(\dfrac{1}{3}.\left(\dfrac{1}{2}-\dfrac{1}{20}\right)\)
=\(\dfrac{1}{3}.\dfrac{9}{20}\)
=\(\dfrac{3}{20}\)
| 2343566365654665456756 | 346549657767736 |
| 6546546546543534654776 | 356547654635646 |
| 5465656546565654654654 | 675687685435346 |
S=\(\dfrac{1}{2.5}+\dfrac{1}{5.8}+....+\dfrac{1}{17.20}\)
=\(\dfrac{1}{3}.\left(\dfrac{3}{2.5}+\dfrac{3}{5.8}+....+\dfrac{3}{17.20}\right)\)
=\(\dfrac{1}{3}.\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{13}+....+\dfrac{1}{14}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{20}\right)\)
=\(\dfrac{1}{3}.\left(\dfrac{1}{2}-\dfrac{1}{20}\right)\)=\(\dfrac{1}{3}.\dfrac{9}{20}\)=\(\dfrac{3}{20}\)
cái này thì mình chx hc nhưng bạn thử tải ứng dụng " photomath " ik