\(\widehat{E}=180^0-\dfrac{1}{2}\left(\widehat{DAB}+\widehat{ABC}\right)\)
\(\widehat{F}=180^0-\dfrac{1}{2}\left(\widehat{ADC}+\widehat{BCD}\right)\)
\(\Leftrightarrow\widehat{E}+\widehat{F}=360^0-\dfrac{1}{2}\cdot360^0=180^0\)
Cho tứ giác lồi ABCD, M, N lần lượt là trung điểm của AB, CD. H là hình chiếu
của M trên CD, K là hình chiếu của N trên AB. CMR SABCD = 1/2
( MH.CD + NK.AB) .
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác
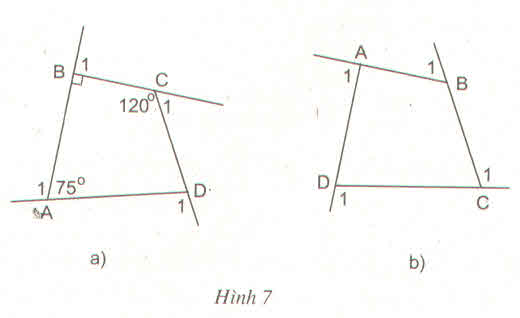
a) Tính các góc ngoài của tứ giác ở hình 7a ?
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : \(\widehat{A_1}+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=?\)
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
BÀI 1 CHO TỨ GIÁC ABCD TRONG ĐÓ CÓ A +B=140 TÍNH TỔNG GÓC C +GÓC D
Tính các góc của hình tứ giác ABCD.
A:B:C:D=1:2:3:4
Cho Tam giác ABC. Trên cùng 1 nửa mặt phẳng bờ BC vẽ tam giac đều ADB, AEC, MBC. Chứng minh rằng: tứ giác ADCE là hình bình hành.
tính các góc của tứ giác ABCD biết ^A:^B:^C:^D=1:2:3:4. Từ đó chứng minh tổng các góc ngoài của tứ giác =360 độ
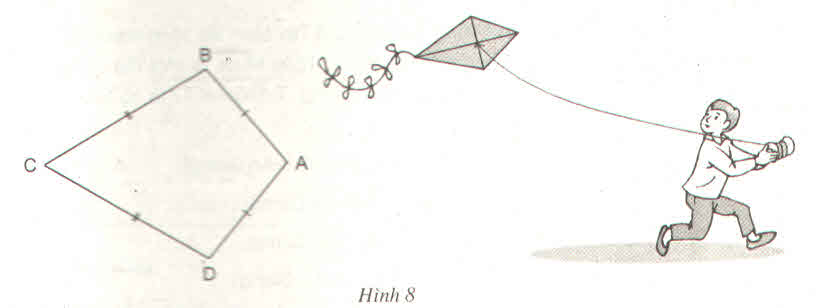
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"
a) Chứng minh rằng AC là đường trung trực của BD
b) Tính \(\widehat{B},\widehat{D}\) biết \(\widehat{A}=100^0,\widehat{C}=60^0\)
1,Cho hình thang ABCD có AB//CD,AB=4 cm,CD=12 cm. Tính độ dài đường trung bình của hình thang.
2,Tam giác ABC vuông tại A , BC = 7cm, MB=MC,M∈BC.Tính AM=?
cho tam gác ABC. trên tia AC lấy điểm D sao cho AD = AB. trên tia AB lấy điểm E sao cho AE = AC chứng minh rằng ABCD là hình thăng
