Trả lời:
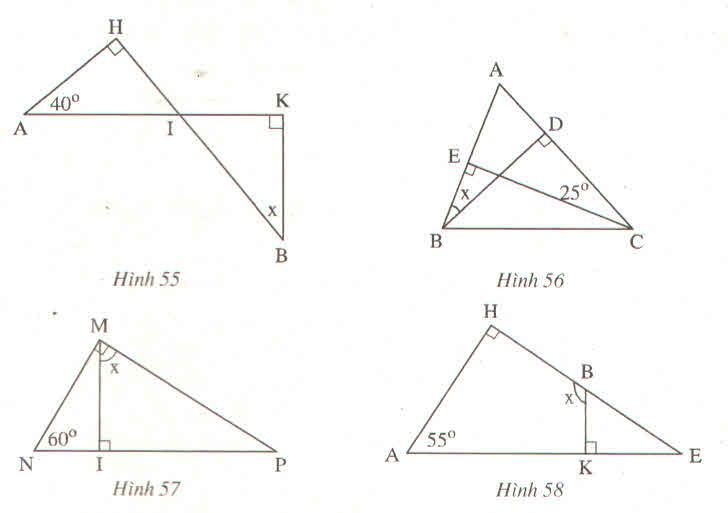
Hình 57:
Ta có: \(\widehat{M_1}+\widehat{M_2}=90^0\),
\(\widehat{N}+\widehat{M_2}=90^0\),
Suy ra \(\widehat{N}=\widehat{M_1}\)
Vậy \(\widehat{M_1}=60^0\)
Hình 58:
Ta có:
\(\widehat{E}=90^0-\widehat{A}=90^0-55^0=35^0\)
\(\widehat{B_1}=90^0+\widehat{E}\) (Góc ngoài tam giác BKE)
= 900 + 350 = 1250
Vậy ...
Chúc bạn học tốt!
Hình 55
\(\widehat{A}+\widehat{AIH}=90^0\)
\(x+\widehat{BIK}=90^0\)
mà \(\widehat{AIH}=\widehat{BIK}\) ( đối đỉnh )
\(\Rightarrow\widehat{A}=x\)
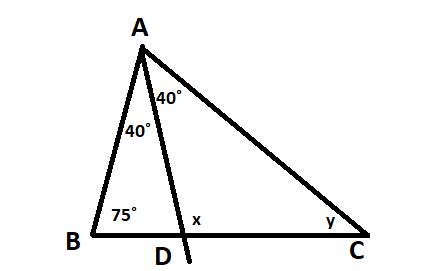
Hình 57
Xét \(\Delta ABD\) cân tại \(D\) ta có \(\Delta ABD+\Delta BAD=90^0\)
Xét \(\Delta ACE\) cân tại \(E\) ta có \(\Delta ACE+\Delta EAC=90^0\)
mà ta có \(\Delta ABD\) cũng chính là góc \(\Delta EAC\)
\(\Rightarrow\Delta ABD=\Delta ACE=25^0\)
Vậy \(\Delta ABD=25^0\Rightarrow x=25^0\)
Chúc bạn học tốt!