c1: EF=5cm
c2: EF=\(5\sqrt{2}\)cm
c3: \(DF=\sqrt{119}cm\)
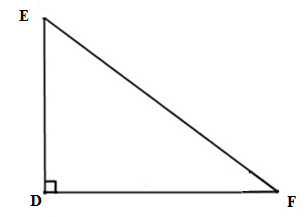
a) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=3^2+4^2\)
=> \(EF^2=9+16\)
=> \(EF^2=25\)
=> \(EF=5\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\left(cm\right).\)
b) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=5^2+5^2\)
=> \(EF^2=25+25\)
=> \(EF^2=50\)
=> \(EF=\sqrt{50}\)
=> \(EF=5\sqrt{2}\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\sqrt{2}\left(cm\right).\)
c) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(12^2=5^2+DF^2\)
=> \(DF^2=12^2-5^2\)
=> \(DF^2=144-25\)
=> \(DF^2=119\)
=> \(DF=\sqrt{119}\left(cm\right)\) (vì \(DF>0\)).
Vậy \(DF=\sqrt{119}\left(cm\right).\)
Chúc bạn học tốt!













