a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và widehat C ge widehat B. Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức {a^2} {b^2} + {c^2} - 2bccos A theo gợi ý sau:Xét tam giác vuông BCD, ta có: {a^2} {d^2} + {(c - x)^2} {d^2} + {x^2} + {c^2} - 2xc (1)Xét tam giác vuông ACD, ta có: {b^2} {d^2} + {x^2} Rightarrow {d^2} {b^2} - {x^2} (2)cos A frac{?}{b} Rightarrow ? bcos A. (3) ...
Đọc tiếp
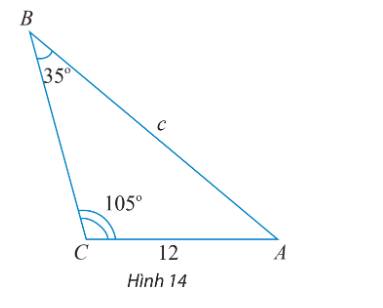
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
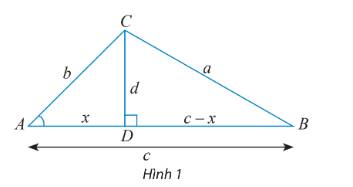
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)