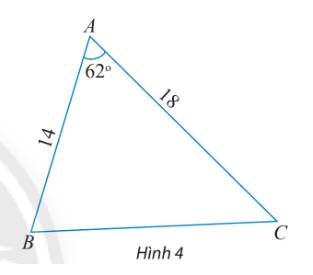
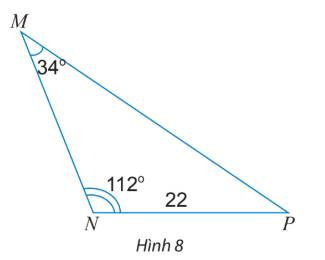
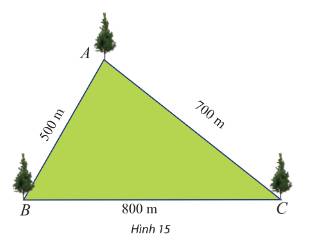
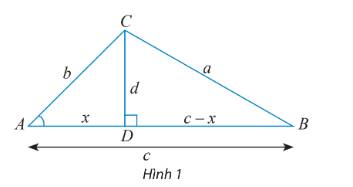
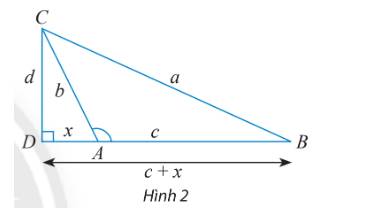
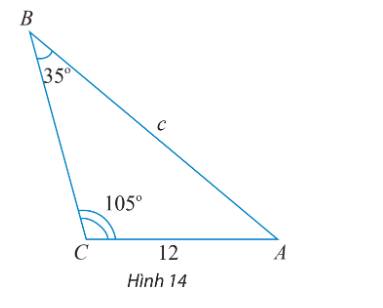
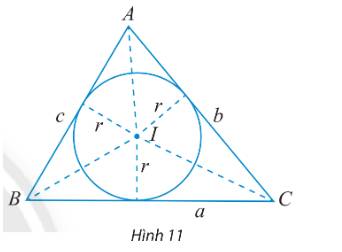
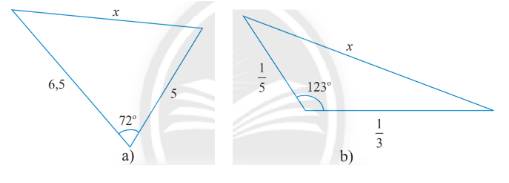
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45'\widehat C \approx {47^o}15'.\)