a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:
\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)
Áp dụng đl cosin, ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
\(\begin{array}{l}
\Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\
\Rightarrow a \approx 30,5
\end{array}\)
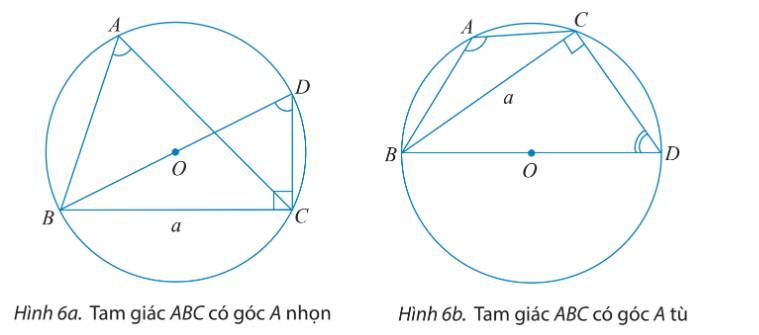
\( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6\)
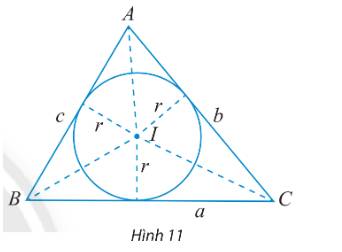
b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {6(6 - 4)(6 - 5)(6 - 3)} = 6.\)
Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.\)