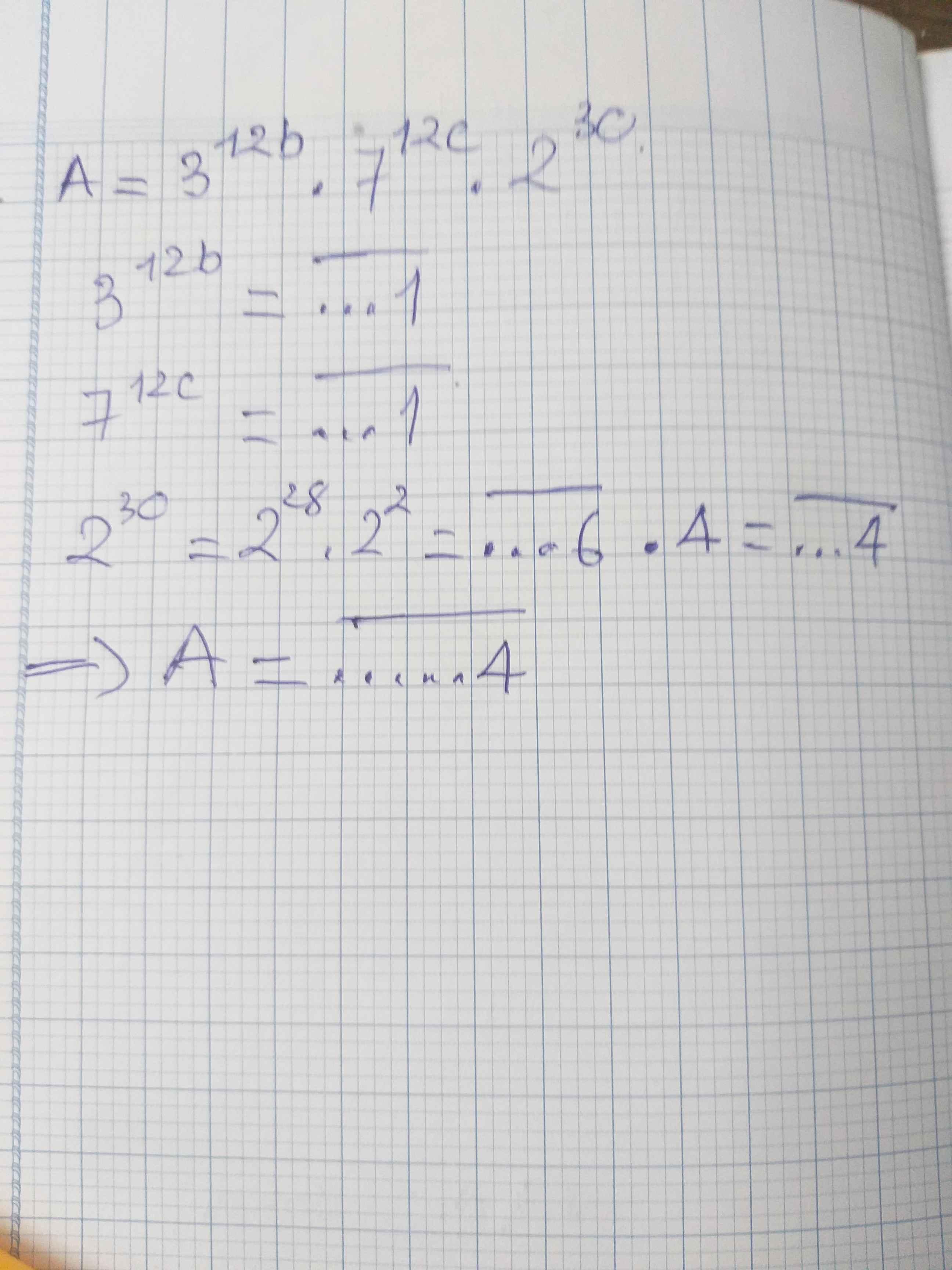Question

tìm số tận cùng của 

a] 3^12 b] 7 ^12 c] 2^ 30 

Answer 1

a) Ta có:

`3^12=3^(3*4)` 

Mà: \(3^{4n}=\overline{....1}\)

`=>3^12` có chữ số tận cùng là 1 

b) Ta có:

`7^12=7^(4*3)`

Mà: \(7^{4n}=\overline{....1}\)  

`=>7^12` có chữ số tận cùng là 1 

c) Ta có: 

`2^30=(2^2)^15`

`=4^15=4^14*4=4^(2*7)*4`

Mà: \(4^{2n}=\overline{...6}\)

`=>\(4^{14}=\overline{...6}\Rightarrow4^{14}\cdot4=\overline{...6}\cdot4=\overline{....4}\)

Vậy: ... 

Answer 2

giúp mình với mình đang vội 

 

Answer 3

Số tận cùng

  

Answer 4

a) 3¹² → chu kỳ tận cùng 3,9,7,1 (4 số) 12 mod 4 = 0 → tận cùng 1 b) 7¹² → chu kỳ 7,9,3,1 12 mod 4 = 0 → tận cùng 1 c) 2³⁰ → chu kỳ 2,4,8,6 30 mod 4 = 2 → tận cùng 4