1 tháng 1 2023 lúc 10:08
Ôn tập cuối năm môn Đại số
Các câu hỏi tương tự
Giải pt
\(1)4x^2+\sqrt{3x+1}+5=13x\)
\(2)7x^2-13x+8=2x^2.\sqrt[3]{x\left(1+3x-3x^2\right)}\)
\(3)x^3-4x^2-5x+6=\sqrt[3]{7x^2+9x-4}\)
\(4)x^3-5x^2+4x-5=\left(1-2x\right)\sqrt[3]{6x^2-2x+7}\)
\(5)8x^2-13x+7=\left(1+\dfrac{1}{x}\right)\sqrt[3]{3x^2-2}\)
Tìm m để \(\left|4x-2m-\dfrac{1}{2}\right|>-x^2+2x+\dfrac{1}{2}-m\) , \(\forall x\)?
Tìm m để mọi nghiệm của bất phương trình x2 - 2(m=1)x + m2 -2m ≤ 0 đều là nghiệm của bất phương trình -x2 + 3x +10 ≥ 0
Tìm GTLN và GTNN [nếu có] của các hàm số; a, y2x2 - 3x+7 với [0;2]...
Đọc tiếp
Tìm GTLN và GTNN [nếu có] của các hàm số; a, y=2x2 - 3x+7 với [0;2] b, y=\((\)x2 +x+2\()\)2 -2x2-2x-1 với x \(\in\)[-1;1] c, y=x2+\(\dfrac{4}{x^2}\) - 3\((x+\dfrac{2}{x})\) +7
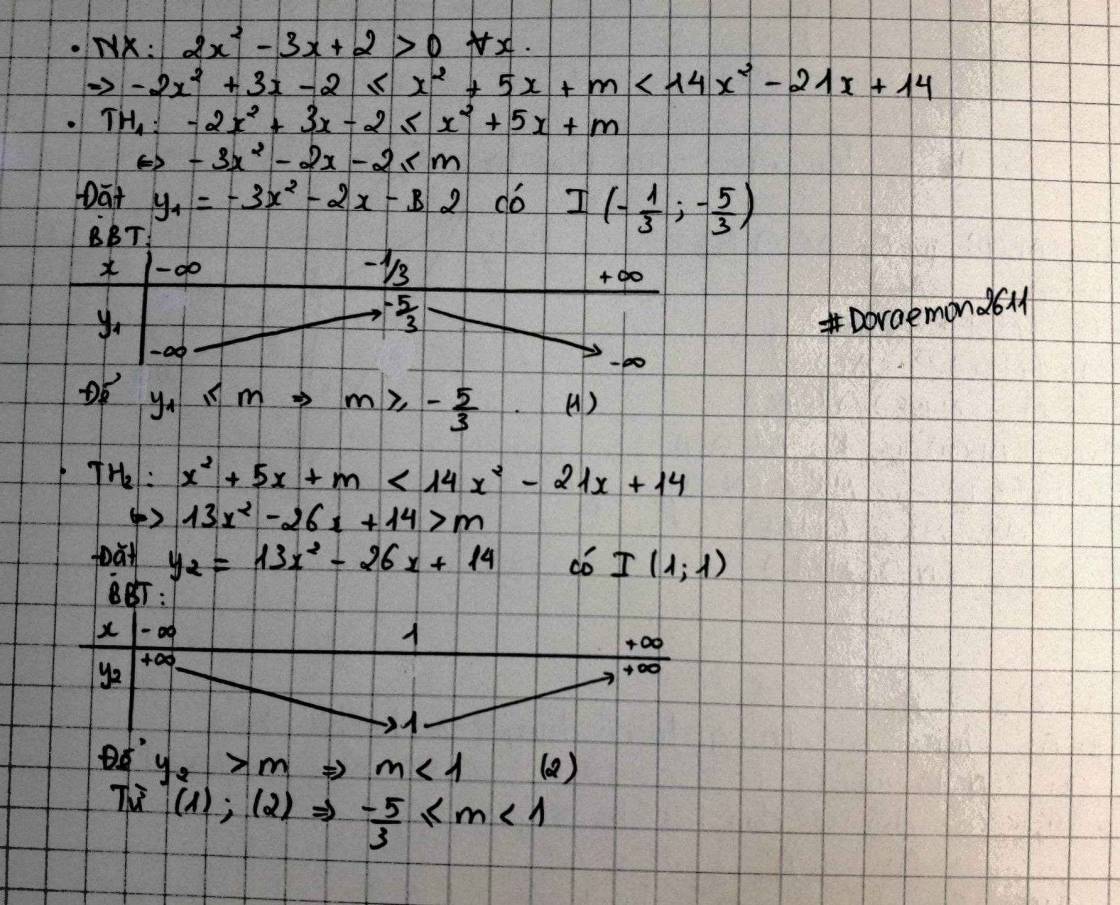
Tìm m để \(\left|\dfrac{x^2+x+4}{x^2-mx+4}\right|\le2\)
Với mọi x thuộc R
Tìm Min của m để \(\dfrac{4x-\sqrt{2x-1}-m}{\sqrt{x^2+\left(m-1\right)^2}-m+1}\le0\) có nghiệm.
tìm tất cả các giá trị của tham số m để bất phương trình sau có No:
\(\sqrt{2+x}+\sqrt{4-x}-\sqrt{8+2x-x^2}\le m\)
tìm tất cả các giá trị của tham số m để bất phương trình sau có No:
\(\sqrt{2+x}+\sqrt{4-x}-\sqrt{8+2x-x^2}\le m\)
Rút gọn :
a) \(\cos\dfrac{x}{5}\cos\dfrac{2x}{5}\cos\dfrac{4x}{5}\cos\dfrac{8x}{5}\)
b) \(\sin\dfrac{x}{7}+2\sin\dfrac{3x}{7}+\sin\dfrac{5x}{7}\)