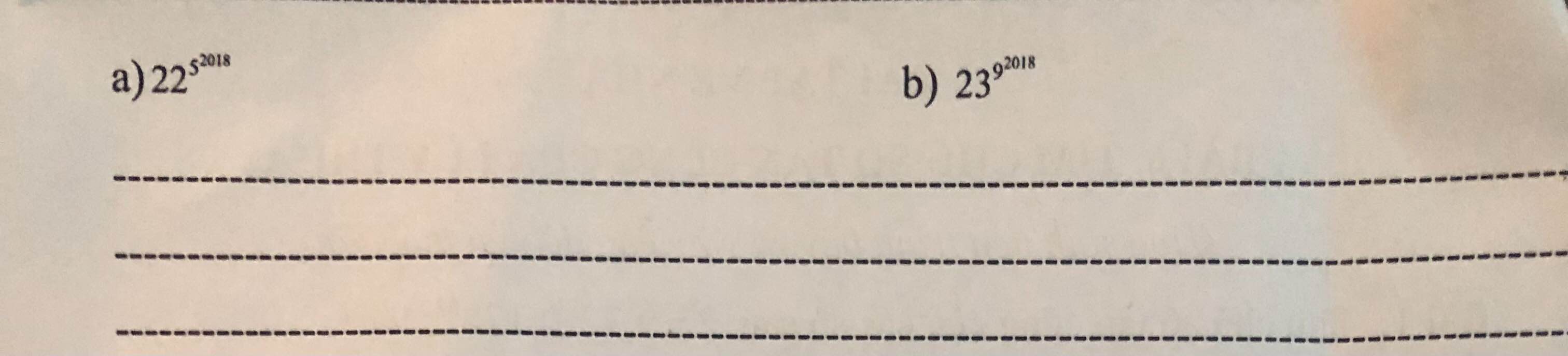Ta có :
Chữ số tận cùng của \(47^5=47\cdot47\cdot47\cdot47\cdot47\) là chữ số tận cùng của \(7\cdot7\cdot7\cdot7\cdot7\) là \(7\)
Nên chữ số tận cùng của số \(47^5\) là \(7\)
Mặt khác: \(2021\) có chữ số tận cùng là \(1\)
Ta có :
\(2021^6=2021\cdot2021\cdot2021\cdot2021\cdot2021\cdot2021\) có chữ số tận cùng của \(1\cdot1\cdot1\cdot1\cdot1\cdot1\) là \(1\)
Vì vậy chữ số tận cùng của số \(2021^6\) là \(1\)
Vậy 475+20216475+20216 có chữ số tận cùng là 7 + 1 = 8.
Các số tự nhiên có chữ số tận cùng là \(\text{0; 1; 2; 3; 4; 5; 6; 7; 8; 9}\) khi bình phương sẽ có chữ số tận cùng lần lượt là \(\text{0; 1; 4; 9; 6; 5; 6; 9; 4; 1}\)
Do đó số chính phương bất kì sẽ có chữ số tận cùng là \(\text{0; 1; 4; 5; 6; 9.}\)
Vậy \(47^5+2021^6\) có chữ số tận cùng là 8 thì không phải là số chính phương.